【题目】如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.
(1)填空:OHOF (“>”、“<”、“=”);
(2)当四边形EFGH为矩形时,请问线段AE与AH应满足什么数量关系;
(3)当四边形EFGH为正方形时,AO与EH交于点P,求OP2+PHPE的最小值.
参考答案:
【答案】
(1)=
(2)
解:当四边形EFGH为矩形时,∠HEF=90°,
∴∠AEH+∠BEF=90°,
在正方形ABCD中,∠HAE=∠EBF=90°,
∴∠AEH+∠AHF=90°,
∴∠AHE=∠BEF,
∴△AEH∽△BFE,
∴ ![]() =
= ![]() ,
,
令AE=x,AH=y,则BF=1﹣y,BE=1﹣x,
∴ ![]() =
= ![]() ,
,
即x﹣y=x2﹣y2=(x+y)(x﹣y),
∴x=y或x+y=1,
∴AE=AH,或AE+AH=1
(3)
解:如图所示,当四边形EFGH为正方形时,∠HOE=90°,OH=OE,
∴∠OEH=∠OHE=45°,
∴∠OHP=∠PAE=45°,
∵∠HPO=∠APE,
∴△OPH∽△EPA,
∴ ![]() =
= ![]() ,即PH×PE=OP×AP,
,即PH×PE=OP×AP,
∴OP2+PH×PE=OP2+OP×AP=OP(OP+AP)=OP×OA,
∵∠OEP=∠OAE=45°,∠POE=∠EOA,
∴△OPE∽△OEA,
∴ ![]() =
= ![]() ,即OP×OA=OE2,
,即OP×OA=OE2,
∴OP2+PH×PE=OE2,
∵当OE⊥AB时,OE最小,此时OE= ![]() ,
,
∴当OE= ![]() 时,OP2+PH×PE最小,且等于
时,OP2+PH×PE最小,且等于 ![]() .
.

【解析】解:(1)如图所示,∵正方形ABCD,
∴AO=CO,∠OAH=∠OCF=45°,
又∵∠AOH=∠COF,
∴△AOH≌△COF,
∴OH=OF;
所以答案是:=;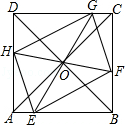
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A. 若∠C=∠A–∠B,则△ABC为直角三角形
B. 若a∶b∶c=2∶2∶2
 ,则△ABC为直角三角形
,则△ABC为直角三角形C. 若a=
 c,b=
c,b= c,则△ABC为直角三角形
c,则△ABC为直角三角形D. 若∠A∶∠B∶∠C=3∶4∶5,则△ABC为直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】龙梅和玉荣是草原上的好朋友,可是有一次经过一场争吵之后,两人不欢而散,龙梅的速度是
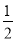 米/秒,4分钟后她停了下来,觉得有点后悔了,玉荣走的方向好像是和龙梅成直角,她的速度是
米/秒,4分钟后她停了下来,觉得有点后悔了,玉荣走的方向好像是和龙梅成直角,她的速度是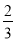 米/秒,如果她和龙梅同时停下来,而这时候她俩正好相距200米,那么她走的方向是否成直角?如果她们现在想讲和,那么原来的速度相向而行,多长时间后能相遇?.
米/秒,如果她和龙梅同时停下来,而这时候她俩正好相距200米,那么她走的方向是否成直角?如果她们现在想讲和,那么原来的速度相向而行,多长时间后能相遇?. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )

①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0)、B(4,﹣1)、C(3,2).
(1)在所给的直角坐标系中画出△ABC;
(2)把△ABC向左平移3个单位,再向上平移2个单位得到△A′B′C′,画出△A′B′C′并写出点C′的坐标;
(3)求△A′B′C′的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB分别切⊙O于A、B两点,点C在优弧
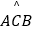 上,∠P=80°,则∠C的度数为( )
上,∠P=80°,则∠C的度数为( ) 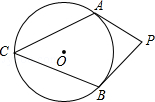
A.50°
B.60°
C.70°
D.80°
相关试题

