【题目】如图,PA、PB分别切⊙O于A、B两点,点C在优弧 ![]() 上,∠P=80°,则∠C的度数为( )
上,∠P=80°,则∠C的度数为( ) 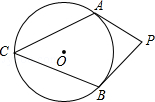
A.50°
B.60°
C.70°
D.80°
参考答案:
【答案】A
【解析】解:∵PA是圆的切线. ∴∠OAP=90°,
同理∠OBP=90°,
根据四边形内角和定理可得:
∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣80°=100°,
∴∠C= ![]() ∠AOB=50°.
∠AOB=50°.
故选A.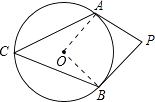
【考点精析】通过灵活运用圆周角定理和切线的性质定理,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,E、F、G、H分别是AB、BC、CD、DA边上的动点(不含端点),且EG、FH均过正方形的中心O.

(1)填空:OHOF (“>”、“<”、“=”);
(2)当四边形EFGH为矩形时,请问线段AE与AH应满足什么数量关系;
(3)当四边形EFGH为正方形时,AO与EH交于点P,求OP2+PHPE的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )

①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0)、B(4,﹣1)、C(3,2).
(1)在所给的直角坐标系中画出△ABC;
(2)把△ABC向左平移3个单位,再向上平移2个单位得到△A′B′C′,画出△A′B′C′并写出点C′的坐标;
(3)求△A′B′C′的面积.

-
科目: 来源: 题型:
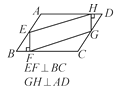
查看答案和解析>>【题目】如图,在平行四边形ABCD中,按下列条件得到的四边形EFGH不一定是平行四边形的是( )
A.
B.

C.

D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以△ABC的两条边为边做平行四边形,所做的平行四边形有____ __个;
平行四边形第四个顶点的坐标是 .

相关试题

