【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.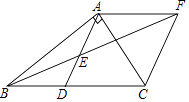
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
参考答案:
【答案】
(1)证明:如图,∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
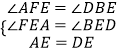 ,
,
∴△AFE≌△DBE(AAS);
∴AF=DB.
∵DB=DC,
∴AF=CD,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC= ![]() BC,
BC,
∴四边形ADCF是菱形;
(2)解:连接DF,
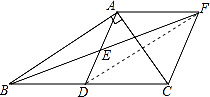
∵AF∥BC,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S= ![]() ACDF=10.
ACDF=10.
【解析】(1)根据已知易证△AFE≌△DBE,得出AF=DB.根据D是BC的中点,得出DB=DC,从而证得AF=CD,可证得四边形ADCF是平行四边形,再根据直角三角形斜边上的中线等于斜边的一半,得出一组邻边相等,即AD=DC,即可证得结论。
(2)先证明四边形ABDF是平行四边形,得出DF的长,根据菱形的面积等于对角线之积的一半,即可求得结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
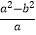 ÷(a﹣
÷(a﹣ 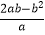 ),其中a=2+
),其中a=2+ 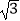 ,b=2﹣
,b=2﹣ 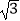 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列因式分解的过程:
(1)x2﹣xy+4x﹣4y
=(x2﹣xy)+(4x﹣4y)(分成两组)
=x(x﹣y)+4(x﹣y)直接提公因式)
=(x﹣y)(x+4)
(2)a2﹣b2﹣c2+2bc
=a2﹣(b2+c2﹣2bc)(分成两组)
=a2﹣(b﹣c)2(直接运用公式)
=(a+b﹣c)(a﹣b+c)
(1)请仿照上述分解因式的方法,把下列各式分解因式:
①
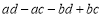
②
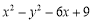
(2)请运用上述分解因式的方法,把多项式1+x+x(1+x)+x(1+x)2+…+x(1+x)n分解因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
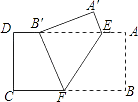
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明. -
科目: 来源: 题型:
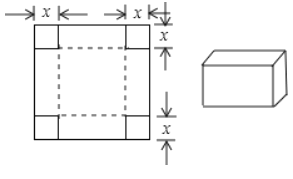
查看答案和解析>>【题目】如图所示,一张边长为
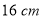 的正方形硬纸板,把它的四个角都剪去一个边长为工
的正方形硬纸板,把它的四个角都剪去一个边长为工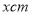 (
(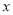 为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为
为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为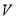 ,请回答下列问题:
,请回答下列问题:(1)用含有
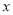 的代数式表示
的代数式表示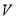 ,则
,则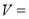
(2)完成下表:
1
2
3
4
5
6
7
(3)观察上表,当
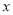 取什么值时,容积
取什么值时,容积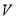 的值最大?
的值最大? -
科目: 来源: 题型:
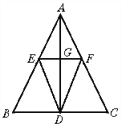
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(—3,—3),B(—2,—1),C(—1,—2)是直角坐标平面上三点。

(1)请画出ΔABC关于原点O对称的ΔA1B1C1,
(2)请写出点B关天y轴对称的点B2的坐标,若将点B2向上平移h个单位,使其落在ΔA1B1C1内部,指出h的取值范围。
相关试题

