【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;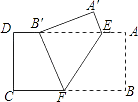
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
参考答案:
【答案】
(1)证明:由题意得B′F=BF,∠B′FE=∠BFE,
在矩形ABCD中,AD∥BC,
∴∠B′EF=∠BFE,
∴∠B′FE=∠B'EF,
∴B′F=B′E,
∴B′E=BF;
(2)解:a,b,c三者存在的关系是a2+b2=c2.
证明:由(1)知B′E=BF=c,A'E=AE=a,
∵B′E=BF=c,
∴在△A'B'E中,∠A=90°,
∴A'E2+A'B'2=B'E2,
∴a2+b2=c2.
【解析】(1)根据折叠的性质得出B′F=BF,∠B′FE=∠BFE,再根据矩形的性质得出AD∥BC,推出∠B′EF=∠BFE,得出∠B′FE=∠B'EF,从而证得B′F=B′E,即可证得结论。
(2)根据题意可知B′E=BF=c,A'E=AE=a,B′E=BF=c,根据勾股定理的逆定理即可证得结论。
【考点精析】利用勾股定理的概念和矩形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象与x轴交于A、B两点,点A的坐标为
的图象与x轴交于A、B两点,点A的坐标为 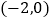 ,求点B的坐标.
,求点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
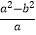 ÷(a﹣
÷(a﹣ 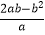 ),其中a=2+
),其中a=2+ 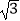 ,b=2﹣
,b=2﹣ 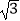 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列因式分解的过程:
(1)x2﹣xy+4x﹣4y
=(x2﹣xy)+(4x﹣4y)(分成两组)
=x(x﹣y)+4(x﹣y)直接提公因式)
=(x﹣y)(x+4)
(2)a2﹣b2﹣c2+2bc
=a2﹣(b2+c2﹣2bc)(分成两组)
=a2﹣(b﹣c)2(直接运用公式)
=(a+b﹣c)(a﹣b+c)
(1)请仿照上述分解因式的方法,把下列各式分解因式:
①
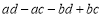
②
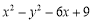
(2)请运用上述分解因式的方法,把多项式1+x+x(1+x)+x(1+x)2+…+x(1+x)n分解因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
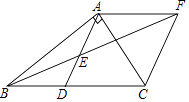
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积. -
科目: 来源: 题型:
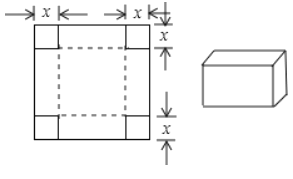
查看答案和解析>>【题目】如图所示,一张边长为
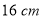 的正方形硬纸板,把它的四个角都剪去一个边长为工
的正方形硬纸板,把它的四个角都剪去一个边长为工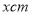 (
(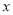 为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为
为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为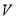 ,请回答下列问题:
,请回答下列问题:(1)用含有
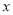 的代数式表示
的代数式表示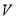 ,则
,则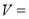
(2)完成下表:
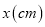
1
2
3
4
5
6
7
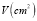
(3)观察上表,当
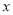 取什么值时,容积
取什么值时,容积 的值最大?
的值最大? -
科目: 来源: 题型:
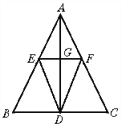
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
相关试题

