【题目】已知a、b、c是△ABC的三边,a、b使等式a2+b2﹣4a﹣8b+20=0成立,且c是偶数,求△ABC的周长.
参考答案:
【答案】10
【解析】
先利用完全平方公式分解因式,进而利用偶次方的性质得出a,b的值,再利用三角形三边关系得出答案.
∵a2+b2-4a-8b+20=0,
∴(a2-4a+4)+(b2-8b+16)=0,
∴(a-2)2+(b-4)2=0,
解得:a=2,b=4,
∵a、b、c是△ABC的三边,且c是偶数,
∴c=4.
故△ABC的周长长为:2+4+4=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断题(下列方程中,是一元二次方程的在括号内划“√”,不是一元二次方程的,在括号内划“×”)|x2+2x|=4 (______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+y=6,xy=5,求下列各式的值:
(1)(x﹣y)2;
(2)x2+y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.

(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠A=45°,∠B=46°,那么△ABC的形状为( )
A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲型H1N1流感病毒的直径约是0.00000011米,用科学记数法表示为___________米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
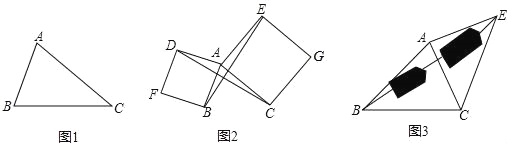
(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写作法,保留作图痕迹);
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.
相关试题

