【题目】某超市计划购进一批甲、乙两种玩具,已知![]() 件甲种玩具的进价与
件甲种玩具的进价与![]() 件乙种玩具的进价的和为
件乙种玩具的进价的和为![]() 元,
元,![]() 件甲种玩具的进价与
件甲种玩具的进价与![]() 件乙种玩具的进价的和为
件乙种玩具的进价的和为![]() 元.
元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过![]() 件,超出部分可以享受
件,超出部分可以享受![]() 折优惠,若购进
折优惠,若购进![]()
![]() 件甲种玩具需要花费
件甲种玩具需要花费![]() 元,请你写出
元,请你写出![]() 与
与![]() 的函数表达式.
的函数表达式.
参考答案:
【答案】(1)每件甲种玩具的进价是30元,每件乙种玩具的进价是27元;(2)当0<x≤20时,y=30x;当x>20时,y=21x+180.
【解析】
(1)设每件甲种玩具的进价是m元,每件乙种玩具的进价是n元,根据“5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元”列出方程组求解即可;
(2)分不大于20件和大于20件两种情况,分别列出函数关系式即可.
解:(1)设每件甲种玩具的进价是m元,每件乙种玩具的进价是n元.
由题意得![]()
解得![]()
答:每件甲种玩具的进价是30元,每件乙种玩具的进价是27元.
(2)当0<x≤20时,y=30x;
当x>20时,y=20×30+(x-20)×30×0.7=21x+180.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.若设甲.乙两种商品原来的单价分别为x元.y元,则可列方程组为_________________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】把
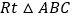 和
和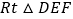 按如图
按如图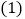 摆放(点
摆放(点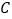 与
与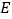 重合),点
重合),点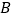 、
、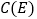 、
、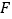 在同一条直线上.已知:
在同一条直线上.已知: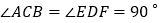 ,
,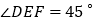 ,
,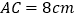 ,
,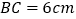 ,
,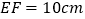 .如图
.如图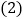 ,
, 从图
从图 的位置出发,以
的位置出发,以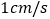 的速度沿
的速度沿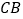 向
向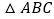 匀速移动,在
匀速移动,在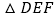 移动的同时,点
移动的同时,点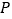 从
从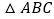 的顶点
的顶点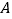 出发,以
出发,以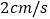 的速度沿
的速度沿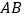 向点
向点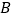 匀速移动;当点
匀速移动;当点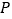 移动到点
移动到点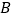 时,点
时,点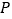 停止移动,
停止移动,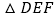 也随之停止移动.
也随之停止移动.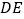 与
与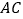 交于点
交于点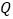 ,连接
,连接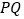 ,设移动时间为
,设移动时间为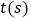 .
.
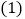 用含
用含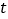 的代数式表示线段
的代数式表示线段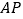 和
和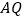 的长,并写出
的长,并写出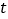 的取值范围;
的取值范围; 当
当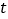 为何值时,
为何值时,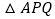 是等腰三角形.
是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学要印制期末考试卷,甲印刷厂提出:每套试卷收0.6元印刷费,另收400元制版费;乙印刷厂提出:每套试卷收1元印刷费,不再收取制版费.
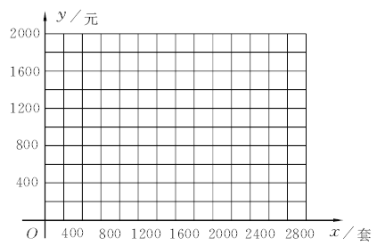
(1)分别写出两个厂的收费y(元)与印刷数量x(套)之间的函数关系式;
(2)请在上面的直角坐标系中分别作出(1)中两个函数的图象;
(3)若学校有学生2000人,为保证每个学生均有试卷,则学校至少要付出印刷费多少元?
-
科目: 来源: 题型:
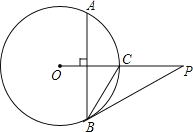
查看答案和解析>>【题目】如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为
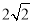 ,求线段EF的长.
,求线段EF的长. -
科目: 来源: 题型:
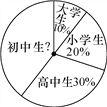
查看答案和解析>>【题目】某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人
捐款 5 元,初中生每人捐款 10 元,高中生每人捐款 15 元,大学生每人捐款 20 元.问平均 每人捐款是多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)——记录下来,则在这组数据中,众数是多少?
相关试题

