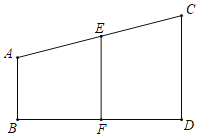
【题目】如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD∥EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由.
证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB= ( )
∴∠ABD+∠CDB=180°
∴AB∥ ( )
又∠A与∠AEF互补 ( )
∠A+∠AEF=
∴AB∥ ( )
∴CD∥EF ( )
参考答案:
【答案】90°;垂直的定义;CD;同旁内角互补,两直线平行;已知;180°;EF;同旁内角互补,两直线平行;平行于同一条直线的两条直线平行.
【解析】
根据同旁内角互补,两直线平行得出AB∥CD,AB∥EF,最后由平行于同一条直线的两条直线平行得出CD∥EF,进而得证.
证明:∵AB⊥BD,CD⊥BD(已知),
∴∠ABD=∠CDB=90°(垂直的定义),
∴∠ABD+∠CDB=180°,
∴AB∥CD(同旁内角互补,两直线平行),
又∠A与∠AEF互补(已知),
∠A+∠AEF=180°,
∴AB∥EF(同旁内角互补,两直线平行),
∴CD∥EF(平行于同一条直线的两条直线平行).
故答案为:90°;垂直的定义;CD;同旁内角互补,两直线平行;已知;180°;EF;同旁内角互补,两直线平行;平行于同一条直线的两条直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
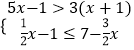 ,并把解集表示在数轴上.
,并把解集表示在数轴上. -
科目: 来源: 题型:
查看答案和解析>>【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
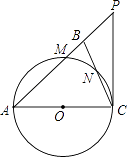
(1)求证:直线CP是⊙O的切线;
(2)若BC=2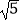 ,sin∠BCP=
,sin∠BCP= 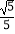 ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=
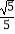 ,BD是AC边上的中线.求:
,BD是AC边上的中线.求: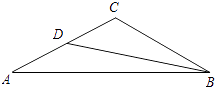
(1)△ABC的面积;
(2)∠ABD的余切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC的一角折叠,使点C落在△ABC内一点
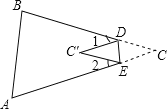
(1)若∠1=40°,∠2=30°,求∠C的度数;(2)试通过第(1)问,直接写出∠1、∠2、∠C三者之间的关系.
相关试题

