【题目】如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.
(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使S△QAM= ![]() S△PDM?若存在,求出点Q的坐标;若不存在,请说明理由.
S△PDM?若存在,求出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)证明:连接CM, 
∵AO是直径,M是圆心,
∴CM=OM,∠ACO=90°,
∴∠MOC=∠MCO.
∵D为OB的中点,
∴CD=OD,
∴∠DOC=∠DCO.
∵∠DOC+∠MOC=90°,
∴∠DCO+∠MCO=90°,
即∠MCD=90°,
∴CD是⊙M的切线
(2)解:方法一:
∵∠ACO=∠AOB=90°,∠OAB=∠OAB,
∴△ACO∽△AOB,
∴ ![]() ,
,
∴ ![]() ,
,
∴AB= ![]() .
.
在Rt△AOB中,由勾股定理,得
BO= ![]() ,
,
∵D为OB的中点,
∴OD= ![]() OB=
OB= ![]() ,
,
∴D(0, ![]() ).
).
∵OM=AM= ![]() OA=
OA= ![]() ,
,
∴M( ![]() ,0).设抛物线的解析式为y=a(x﹣
,0).设抛物线的解析式为y=a(x﹣ ![]() )(x﹣5),由题意,得
)(x﹣5),由题意,得
![]() =a(0﹣
=a(0﹣ ![]() )(0﹣5),
)(0﹣5),
解得:a= ![]() ,
,
∴抛物线的解析式为:y= ![]() (x﹣
(x﹣ ![]() )(x﹣5),
)(x﹣5),
= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() .
.
连接AD交对称轴于P,设直线AD的解析式为y=kx+b,由题意,得
 ,
,
解得:  ,
,
∴直线AD的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
当x= ![]() 时,
时,
y= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
方法二:
∵OA=5,AC=3,∠ACO=90°,
∴OC=4,tan∠CAO= ![]() ,
,
∴OB= ![]() ,
,
∵D为BO的中点,
∴D(0, ![]() ),M(
),M( ![]() ,0),A(5,0),
,0),A(5,0),
∴设抛物线的解析式为:y=a(x﹣ ![]() )(x﹣5),
)(x﹣5),
把D(0, ![]() )代入得a=
)代入得a= ![]() ,
,
∴抛物线的解析式为:y= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∵P为对称轴上一点,
∴PM=PA,
∴△PDM的周长最小时,D,P,A三点共线,
∵D(0, ![]() ),A(5,0),
),A(5,0),
∴lAD:y=﹣ ![]() x+
x+ ![]() ,
,
当x= ![]() 时,y=
时,y= ![]() ,
,
∴P( ![]() ,
, ![]() ).
).
(3)解:存在.
∵S△PDM=S△ADM﹣S△APM,
∴S△PDM= ![]() ×
× ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]() ×
× ![]() ,
,
= ![]() ,
,
∴S△QAM= ![]() =
= ![]() .
.
设Q的纵坐标为m,由题意,得
![]() ,
,
∴|m|= ![]() ,
,
∴m=± ![]() ,
,
当m= ![]() 时,
时,
![]() =
= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() .
.
x1= ![]() ,x2=
,x2= ![]() ,
,
当m=﹣ ![]() 时,
时,
﹣ ![]() =
= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() .
.
x= ![]() .
.
∴Q( ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() ),(
),( ![]() ,﹣
,﹣ ![]() ).
).
【解析】本题是一道二次函数与几何的综合题.解答此题的关键是求出抛物线的解析式.
(1)连接CM,由题意易得CM=OM,从而得到∠MOC=∠MCO,由OA为直径,根据圆周角的推论可得∠ACO=90°,易证CD=OD,∠DOC=∠DCO,由∠DOC+∠MOC=90°就可得∠DCO+∠MCO=90°,从而可得结论;
(2)根据已知条件可得△ACO∽△AOB求得AC:AO=AO:AB,从而求出AB,在Rt△AOB中由勾股定理求出OB的长,根据D是OB的中点可求得D的坐标,由待定系数法就可求得抛物线的解析式,从而求出其对称轴,连接AD交对称轴于P,先求出AD的解析式就可得点P的坐标;
(3)根据S△PDM=S△ADM-S△APM,可求得△PDM的面积,从而表示出△QAM面积的大小,设Q的纵坐标为m,根据三角形的面积可求出Q的横坐标,即可得
【考点精析】掌握圆周角定理和切线的判定定理是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2 , 后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
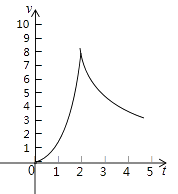
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=ABAE.
求证:DE是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连结CQ.若PA∶PB∶PC=3∶4∶5,连结PQ,试判断△PQC的形状( )

A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
-
科目: 来源: 题型:
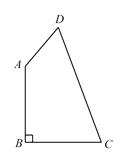
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△A′B′C′是△ABC 经过平移得到的,△ABC 中任意一点 P(x1,y1)平移后的对应点为 P′(x1+6,y1﹣5).
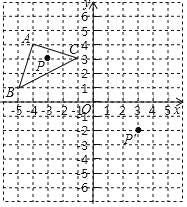
(1)请写出三角形 ABC 平移的过程;
(2)分别写出点 A′,B′,C′的坐标;
(3)画出平移后的图形.
相关试题

