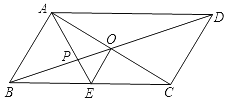
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,分别交BC,BD于点E,P,连接OE,∠ADC=60°,AB=![]() BC=2,下列结论:①∠CAD=30°;②BD=2
BC=2,下列结论:①∠CAD=30°;②BD=2![]() ;③S四边形ABCD=ABAC;④OE=
;③S四边形ABCD=ABAC;④OE=![]() AD;⑤S△BOE=
AD;⑤S△BOE=![]() .其中正确的个数有( )个
.其中正确的个数有( )个
A.2B.3C.4D.5
参考答案:
【答案】D
【解析】
①先根据角平分线和平行线的性质得:∠BAE=∠BEA,则AB=BE=2,由有一个角是60度的等腰三角形是等边三角形得:△ABE是等边三角形,由外角的性质和等腰三角形的性质得:∠ACE=30°,最后由平行线的性质可作判断;
②先根据三角形中位线定理得:OE=![]() AB=1,OE∥AB,根据勾股定理计算OC,OD的长,即可求BD的长;
AB=1,OE∥AB,根据勾股定理计算OC,OD的长,即可求BD的长;
③因为∠BAC=90°,根据平行四边形的面积公式可作判断;
④根据三角形中位线定理可作判断;
⑤由三角形中线的性质可得:S△BOE=S△EOC=![]() OEOC=
OEOC=![]() .
.
解:①∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC=60°,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE=2,
∴△ABE是等边三角形,
∴AE=BE=2,
∵BC=4,
∴EC=2,
∴AE=EC,
∴∠EAC=∠ACE,
∵∠AEB=∠EAC+∠ACE=60°,
∴∠ACE=30°,
∵AD∥BC,
∴∠CAD=∠ACE=30°,
故①正确;
②∵BE=EC,OA=OC,
∴OE=![]() AB=1,OE∥AB,
AB=1,OE∥AB,
∴∠EOC=∠BAC=60°+30°=90°,
Rt△EOC中,OC=![]() ,
,
∵四边形ABCD是平行四边形,
∴∠BCD=∠BAD=120°,
∴∠ACB=30°,
∴∠ACD=90°,
Rt△OCD中,OD=![]()
BD=2OD=2![]()
故②正确
③由②知:∠BAC=90°,
∴SABCD=ABAC,
故③正确;
④由②知:OE是△ABC的中位线,
∴OE=![]() AB,
AB,
∵AB=![]() BC,
BC,
∴OE=![]() BC=
BC=![]() AD,
AD,
故④正确;
⑤∵BE=EC=2
∴S△BOE=S△EOC=![]() OEOC=
OEOC=
故⑤正确
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )

A.8B.6C.4D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】高考英语听力测试期间,需要杜绝考点周围的噪音.如图,点A是某市一高考考点,在位于A考点南偏西15°方向距离125米的C处有一消防队.在听力考试期间,消防队突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即赶往救火.已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改进行驶,试问:消防车是否需要改道行驶?请说明理由.(
 取1.732)
取1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶
小瓶
进价(元/瓶)
5
2
售价(元/瓶)
7
3
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABCO的顶点A、C分别在直线x=2和x=7上,O是坐标原点,则对角线OB长的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.
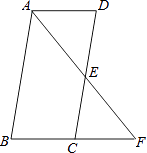
(1)求证:△ADE和△CEF的面积相等;
(2)若AB=2AD,试说明AF恰好是∠BAD的平分线. -
科目: 来源: 题型:
查看答案和解析>>【题目】足球是世界第一运动,参与足球运动可以锻炼身体,陶冶情操.“高新美少年,阳春蹴鞠忙”,让学生走出教室,走进阳光,让每一位学生健康、快乐成长,是高新一中初中校区一直秉承的理念.本月,我校第四届校园足球联赛落下了帷幕,并取得了四满成功.为了举办本次活动,我校在商场购买甲、乙两种不同的足球,购买甲种足球共花费2600元,购买乙种足球共花费1328元,购买甲种足球的数量是购买乙种足球数量的2.5倍,且购买一个乙种足球比购买一个甲种足球多花18元.求购买一个甲种足球、一个乙种足球各需多少元?
相关试题

