【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于E,BD交CE于点F,
的中点,CE⊥AB于E,BD交CE于点F,
(1)求证:CF=BF;
(2)若CD=12,AC=16,求⊙O的半径和CE的长.

参考答案:
【答案】(1)证明见解析(2)10,9.6
【解析】
试题分析:(1)由AB是⊙O的直径,CE⊥AB,易得∠2=∠A,又由C是,![]() 的中点,可得∠1=∠A,即可得∠1=∠2,判定CF=BF;
的中点,可得∠1=∠A,即可得∠1=∠2,判定CF=BF;
(2)由C是![]() 的中点,可得BC=CD=12,又由AB是⊙O的直径,可得∠ACB=90°,即可求得AB的长,然后由三角的面积,求得CE的长.
的中点,可得BC=CD=12,又由AB是⊙O的直径,可得∠ACB=90°,即可求得AB的长,然后由三角的面积,求得CE的长.
试题解析:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
又∵CE⊥AB,
∴∠CEB=90°,
∴∠2=90°﹣∠ABC=∠A,
又∵C是弧BD的中点,
∴∠1=∠A,
∴∠1=∠2,
∴CF=BF;
(2)∵C是弧BD的中点,
∴![]() ,
,
∴BC=CD=12,
又∵在Rt△ABC中,AC=16,
∴由勾股定理可得:AB=20,
∴⊙O的半径为10,
∵S△ABC=![]() ACBC=
ACBC=![]() ABCE,
ABCE,
∴CE=![]() =9.6.
=9.6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2y﹣4y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲地的海拔高度是300m,乙地的海拔高度是﹣50m,那么甲地比乙地高m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l上有A、B两点,AB=24cm,点O是线段AB上的一点,OA=2OB.

(1)OA=cm,OB=cm.
(2)若点C是线段AO上一点,且满足AC=CO+CB,求CO的长.
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为t(s),当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP﹣OQ=8.
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后立即返回,又以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程为cm. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3﹣2a=aB.a2a3=a6
C.(a2)3=a6D.﹣(a﹣1)=﹣a﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣7xm+2y与﹣3x3yn是同类项,则m= , n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起.
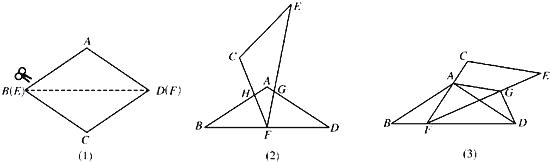
(1)操作:如图2,将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,设旋转时FC交BA于点H(H点不与B点重合),FE交DA于点G(G点不与D点重合).
求证:BHGD=BF2
(2)操作:如图3,△ECF的顶点F在△ABD的BD边上滑动(F点不与B、D点重合),且CF始终经过点A,过点A作AG∥CE,交FE于点G,连接DG.
探究:FD+DG= .请予证明.
相关试题

