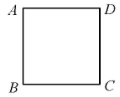
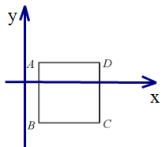
【题目】数学课上,王老师让同学们对给定的正方形![]() ,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
,建立合适的平面直角坐标系,并表示出各顶点的坐标.下面是4名同学表示各顶点坐标的结果:
甲同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
乙同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
丙同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
丁同学:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
上述四名同学表示的结果中,四个点的坐标都表示正确的同学是__________.
参考答案:
【答案】甲、丙、丁
【解析】
根据A、B两点坐标,构建直角坐标系,然后验证C、D两点是否正确即可
甲同学,以点B为坐标原点,1作为正方形的边长,坐标轴图下图:
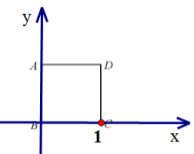
则A(0,1),C(1,0),D(1,1),甲同学正确;
乙同学,以点A为坐标原点,1作为正方形边长
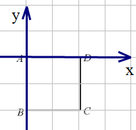
则:B(0,-1),C(1,-1),D(1,0),乙同学错误;
丙同学,以点B为坐标原点,3作为正方形的边长,
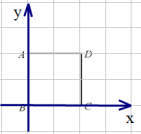
则A(0,3),C(3,0),D(3,3),丙同学正确;
丁同学,3作为正方形边长,以点A下方距离1、左方距离1的位置为原点,
则![]() ,
,![]() ,
,![]() ,
,![]() ,丁正确
,丁正确
故答案为:甲、丙、丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
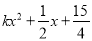 (k是常数).
(k是常数).(1)若该函数的图象与x轴有两个不同的交点,试求k的取值范围;
(2)若点(1,k)在某反比例函数图象上,要使该反比例函数和二次函数y=
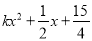 都是y随x的增大而增大,求k应满足的条件及x的取值范围;
都是y随x的增大而增大,求k应满足的条件及x的取值范围;(3)若抛物线y=
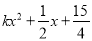 与x轴交于A(
与x轴交于A(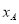 ,0)、B(
,0)、B(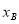 ,0)两点,且
,0)两点,且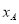 <
<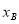 ,
, =34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于
=34,若与y轴不平行的直线y=ax+b经过点P(1,3),且与抛物线交于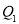 (
(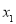 ,
,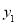 )、
)、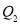 (
( ,
,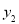 )两点,试探究
)两点,试探究 是否为定值,并写出探究过程.
是否为定值,并写出探究过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在国家大数据战略的引领下,我国在人工智能领域取得显著成就,自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,它们决定着人工智能深度学习的质量和速度,其中的一个大数据中心能存储580亿本书籍,将580亿用科学记数法表示应为( ).
A.
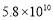 B.
B.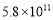 C.
C.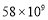 D.
D.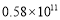
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是2020年3月26日全国新冠疫情数据表,图2是3月28日海外各国疫情统计表,图3是中国和海外的病死率趋势对比图,根据这些图表,选出下列说法中错误的一项( )


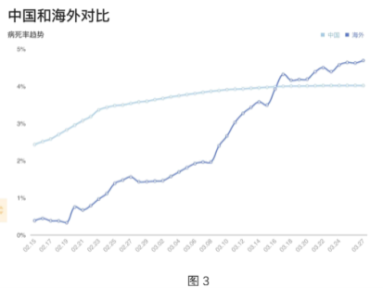
A.图1显示每天现有确诊数的增加量=累计确诊增加量-治愈人数增加量-死亡人数增加量.
B.图2显示美国累计确诊人数虽然约是德国的两倍,但每百万人口的确诊人数大约只有德国的一半.
C.图2显示意大利当前的治愈率高于西班牙.
D.图3显示大约从3月16日开始海外的病死率开始高于中国的病死率
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品
顾客人数
甲
乙
丙
丁
100
√
×
√
√
217
×
√
×
√
200
√
√
√
×
300
√
×
√
×
85
√
×
×
×
98
×
√
×
×
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
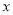 的方程
的方程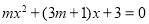 .
.(1)求证:不论
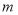 为任何实数,此方程总有实数根;
为任何实数,此方程总有实数根;(2)若抛物线
 与
与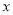 轴交于两个不同的整数点,且
轴交于两个不同的整数点,且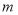 为正整数,试确定此抛物线的解析式.
为正整数,试确定此抛物线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF =∠BAE.
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
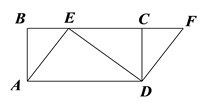
相关试题

