【题目】如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( ) 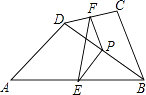
A.15°
B.20°
C.25°
D.30°
参考答案:
【答案】D
【解析】解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点, ∴FP,PE分别是△CDB与△DAB的中位线,
∴PF= ![]() BC,PE=
BC,PE= ![]() AD,
AD,
∵AD=BC,
∴PF=PE,
故△EPF是等腰三角形.
∵∠PEF=30°,
∴∠PEF=∠PFE=30°.
故选:D.
【考点精析】认真审题,首先需要了解三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红每分钟踢毽子的次数正常范围为少于80次,但不少于50次,用不等式表示为( )
A. 50<x<80; B. 50≤x≤80; C. 50≤x<80; D. 50<x≤80;
-
科目: 来源: 题型:
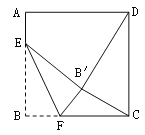
查看答案和解析>>【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
(1)当∠BEF=45°时,求证:CF=AE;
(2)当B′D=B′C时,求BF的长;
(3)求△CB′F周长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将二次函数y=(x﹣2)2+2的图象向左平移2个单位,所得图象对应的函数解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2x﹣5y=0,则x:y的值为( )
A.2:5B.5:2C.3:2D.2:3
-
科目: 来源: 题型:
查看答案和解析>>【题目】新华购物中心新购进篮球和排球共30个,进价和售价如表,全部销售完后共获利润510元.
篮球
排球
进价(元/个)
95
80
售价(元/个)
110
100
(1)购进篮球和排球各多少个?
(2)销售8个排球的利润与销售几个篮球的利润相等? -
科目: 来源: 题型:
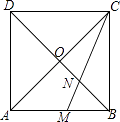
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( )
A.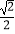
B.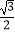
C.1
D.
相关试题

