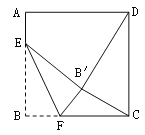
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
(1)当∠BEF=45°时,求证:CF=AE;
(2)当B′D=B′C时,求BF的长;
(3)求△CB′F周长的最小值.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)△CB′F周长的最小值为
;(3)△CB′F周长的最小值为![]() .
.
【解析】(1)利用正方形的性质即可证得结论;(2)运用翻折的性质在Rt△B′MF中运用勾股定理BF的长;(3)根据折叠的对称性求出△CB′F周长的最小值.
(1)证明:
∵ABCD是正方形,
∴∠B=90°,AB=BC,
∵∠BEF=45°,
∴∠BFE=∠BEF=45°,
∴BE=BF,
∴AE=CF.
(2)如图1,过B′点作GH∥AD,分别交AB、CD于点G、H,则∠B′GE=90°.
∵B′C=B′D,

∴DH=AG=![]() DC=8,
DC=8,
∵AE=3,AB=16,
∴BE=13,
由翻折的性质可得:B′E=BE=13.
∴ EG=AG﹣AE=8﹣3=5,
∴ B′G=![]() ,
,
过B′点作B′M∥BC交BC于点M,
则B′M=BG=8.BM=B′G=12,
设BF= ![]() ,则B′F=BF=
,则B′F=BF= ![]() ,FM=12﹣
,FM=12﹣![]() ,
,
在Rt△B′MF中,∠B′MF=90°,
∴ B′F2= FM2+ B′M2,
即![]() ,
,
解得: ![]() ,即BF =
,即BF =![]() .
.
(3)如图2.
∵FB′+ FC=BC=16,
∴当CB′最小时,△CB′F的周长也最小,

而当C、B′、E三点共线时,CB′取最小值,
此时CB′=CE-EB′=![]() ,
,
∴△CB′F周长的最小值为![]() .
.
或∵FB′+ FC=BC=16,
∴当CB′最小时,△CB′F的周长也最小,
当∠CB′F=90°时,CB′最小,
而这时C、B′、E三点共线,
此时CB′=CE-EB′=![]() ,
,
∴△CB′F周长的最小值为![]() .
.
“点睛”本题考查了正方形的性质、翻折的性质、折叠的对称性,灵活运用性质是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)若该客户按方案①购买,需付款元(用含x的代数式表示);
若该客户按方案②购买,需付款元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算? -
科目: 来源: 题型:
查看答案和解析>>【题目】周六妈妈从新世纪购物回来,5斤蘑菇和1斤牛肉共40元,妈妈唠叨:“上周也是买同样多才花了35元,价格上涨太厉害了.”在看书的爸爸:“刚才听老张说蘑菇单价上涨40%,牛肉单价上涨10%”,在学习的小强想应该怎样通过列方程(组)求解今天蘑菇、牛肉的单价呢?请聪明的你帮小强解决这个问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红每分钟踢毽子的次数正常范围为少于80次,但不少于50次,用不等式表示为( )
A. 50<x<80; B. 50≤x≤80; C. 50≤x<80; D. 50<x≤80;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将二次函数y=(x﹣2)2+2的图象向左平移2个单位,所得图象对应的函数解析式为_____.
-
科目: 来源: 题型:
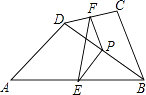
查看答案和解析>>【题目】如图,在四边形ABCD中,点P是对角线BD的中点,点E,F分别是AB,CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( )
A.15°
B.20°
C.25°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2x﹣5y=0,则x:y的值为( )
A.2:5B.5:2C.3:2D.2:3
相关试题

