【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( ) 
A.2
B.3
C.4
D.5
参考答案:
【答案】D
【解析】解:∵正方形ABCD的边长为6,CE=2DE,
∴DE=2,EC=4,
∵把△ADE沿AE折叠使△ADE落在△AFE的位置,
∴AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,
在Rt△ABG和Rt△AFG中![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),
∴GB=GF,∠BAG=∠FAG,
∴∠GAE=∠FAE+∠FAG= ![]() ∠BAD=45°,所以①正确;
∠BAD=45°,所以①正确;
设BG=x,则GF=x,C=BC﹣BG=6﹣x,
在Rt△CGE中,GE=x+2,EC=4,CG=6﹣x,
∵CG2+CE2=GE2 ,
∴(6﹣x)2+42=(x+2)2 , 解得x=3,
∴BG=3,CG=6﹣3=3
∴BG=CG,所以②正确;
∵EF=ED,GB=GF,
∴GE=GF+EF=BG+DE,所以③正确;
∵GF=GC,
∴∠GFC=∠GCF,
又∵Rt△ABG≌Rt△AFG,
∴∠AGB=∠AGF,
而∠BGF=∠GFC+∠GCF,
∴∠AGB+∠AGF=∠GFC+∠GCF,
∴∠AGB=∠GCF,
∴CF∥AG,所以④正确;
过F作FH⊥DC
∵BC⊥DH,
∴FH∥GC,
∴△EFH∽△EGC,
∴ ![]() ,
,
EF=DE=2,GF=3,
∴EG=5,
∴△EFH∽△EGC,
∴相似比为: ![]() =
= ![]() ,
,
∴S△FGC=S△GCE﹣S△FEC= ![]() ×3×4﹣
×3×4﹣ ![]() ×4×(
×4×( ![]() ×3)=
×3)= ![]() =3.6,所以⑤正确.
=3.6,所以⑤正确.
故正确的有①②③④⑤,
故选:D.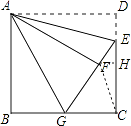
【考点精析】本题主要考查了正方形的性质和翻折变换(折叠问题)的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一直角坐标系中,函数y=
 与y=kx+k2的大致图象是( )
与y=kx+k2的大致图象是( )
A.
B.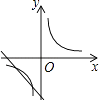
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10cm;BC=6cm,点D为AB的中点.
(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B出发都逆时针沿△ABC三边运动,直接写出经过多少秒后,点P与点Q第一次在△ABC的那一条边上相遇.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于( )

A.1
B.2
C.4
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2016﹣
 +(cos60°)﹣1+(
+(cos60°)﹣1+(  ﹣
﹣  )0+83×(﹣0.125)3 .
)0+83×(﹣0.125)3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等腰三角形,AB=AC,∠D=∠E,∠BAD=∠CAE.
(1)写出一对全等的三角形:△ ≌△ ;
(2)证明(1)中的结论;
(3)求证:点G为BC的中点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠C=90°,D是AB的中点,DE⊥DF,点E,F分别在AC,BC上,求证:DE=DF.

相关试题

