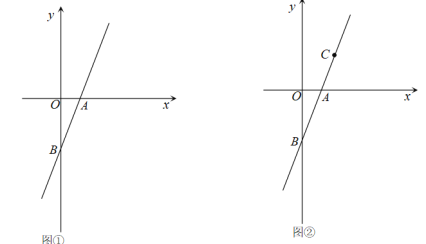
【题目】已知,直线y=2x-2与x轴交于点A,与y轴交于点B.
(1)如图①,点A的坐标为_______,点B的坐标为_______;
(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.
①求点C的坐标;
②过动点P(m,0)且垂直与x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是_______;
(3)若∠ABN=45,求直线BN的解析式.
参考答案:
【答案】(1)(1,0),(0,-2);(2)C(2,2);m<0或m>2;(3)![]() 或y=-3x-2.
或y=-3x-2.
【解析】
(1)利用函数解析式和坐标轴上点的坐标特征即可解决问题;
(2)①如图②,过点C 作CD⊥x 轴,垂足是D.构造全等三角形,利用全等三角形的性质求得点C的坐标;
②由①可知D(2,0),观察图②,可知m的取值范围是:m<0或m>2;
(3)如图③中,作AN⊥AB,使得AN=AB,作NH⊥x轴于H,则△ABN是等腰直角三角形,∠ABN=45°.利用全等三角形的性质求出点N坐标,当直线BN′⊥直线BN时,直线BN′也满足条件,求出直线BN′的解析式即可.
解:(1)如图①,

令y=0,则2x-2=0,即x=1.所以A(1,0).
令x=0,则y=-2,即B(0,-2).
故答案是:(1,0);(0,-2);
(2)①如图②,

过点C 作CD⊥x 轴,垂足是D,
∵∠BOA=∠ADC=90°,
∠BAO=∠CAD,
CA=AB,
∴△BOA≌△CAD(AAS),
∴CD=OB=2,AD=OA=1,
∴C(2,2);
②由①可知D(2,0),观察图②,可知m的取值范围是:m<0或m>2.
故答案是:m<0或m>2;
(3)如图③,作AN⊥AB,使得AN=AB,作NH⊥x轴于H,则△ABN是等腰直角三角形,∠ABN=45°.

∵∠AOB=∠BAN=∠AHN=90°,
∴∠OAB+∠ABO=90°,∠OAB+∠HAN=90°,
∴∠ABO=∠HAN,
∵AB=AN,
∴△ABO≌△NAH(AAS),
∴AH=OB=2,NH=OA=1,
∴N(3,-1),
设直线BN的解析式为y=kx+b,
则有:![]() ,
,
解得 ,
,
∴直线BN的解析式为y=![]() x-2,
x-2,
当直线BN′⊥直线BN时,直线BN′也满足条件,直线BN′的解析式为:
![]() .
.
∴满足条件的直线BN的解析式为y=![]() x-2或y=-3x-2.
x-2或y=-3x-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.
(1)根据题意,填写下表:
快递物品重量(千克)
0.5
1
3
4
…
甲公司收费(元)
22
…
乙公司收费(元)
11
51
67
…
(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种水果的价格如表:
购买的质量(千克)
不超过10千克
超过10千克
每千克价格
6元
5元
张欣两次共购买了25千克这种水果(第二次多于第一次),共付款132元.问张欣第一次、第二次分别购买了多少千克这种水果?
-
科目: 来源: 题型:
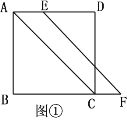
查看答案和解析>>【题目】已知,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,且AE=CF,连接AC,EF.
(1)如图①,求证:EF//AC;
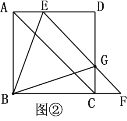
(2)如图②,EF与边CD交于点G,连接BG,BE,
①求证:△BAE≌△BCG;
②若BE=EG=4,求△BAE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算与简化:
(1)﹣22﹣[(1﹣1×0.6)+(﹣0.2)2﹣4]
(2)
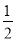 (2a2﹣9b)﹣3(﹣5a2﹣
(2a2﹣9b)﹣3(﹣5a2﹣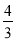 b)﹣3b
b)﹣3b(3)x﹣
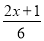 =
=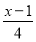 +2
+2(4)
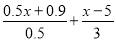 =
=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=

求:(1)反比例函数的解析式;
(2)点C的坐标;
(3)sin∠ABC的值.

相关试题

