【题目】计算与简化:
(1)﹣22﹣[(1﹣1×0.6)+(﹣0.2)2﹣4]
(2)![]() (2a2﹣9b)﹣3(﹣5a2﹣
(2a2﹣9b)﹣3(﹣5a2﹣![]() b)﹣3b
b)﹣3b
(3)x﹣![]() =
=![]() +2
+2
(4)![]() =
=![]()
参考答案:
【答案】(1)﹣0.44;(2)16a2﹣![]() b;(3)x=
b;(3)x=![]() ;(4)x=
;(4)x=![]()
【解析】
(1)根据有理数的混合运算的法则计算即可;
(2)根据整式的混合运算的法则计算即可;
(3)首先去分母、然后去括号、移项、合并同类项、最后化系数为1即可求解;
(4)首先根据分式的基本性质化简方程,然后去分母、然后去括号、移项、合并同类项、最后化系数为1即可求解.
(1)原式=﹣4﹣0.4﹣0.04+4=﹣0.44;
(2)原式=a2﹣![]() b+15a2+4b﹣3b
b+15a2+4b﹣3b
=16a2﹣![]() b;
b;
(3)去分母得:12x﹣4x﹣2=3x﹣3+24,
移项合并得:5x=23,
解得:x=![]() ;
;
(4)方程整理得:![]() =
=![]() ,
,
去分母,得3(5x+9)+5(x﹣5)=5(1+2x),
去括号,得15x+27+5x﹣25=5+10x,
移项,得15x+5x﹣10x=﹣27+25+5,
合并同类项,得10x=3,
系数化为1得x=![]() .
.
-
科目: 来源: 题型:
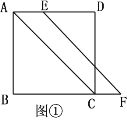
查看答案和解析>>【题目】已知,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,且AE=CF,连接AC,EF.
(1)如图①,求证:EF//AC;
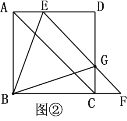
(2)如图②,EF与边CD交于点G,连接BG,BE,
①求证:△BAE≌△BCG;
②若BE=EG=4,求△BAE的面积.
-
科目: 来源: 题型:
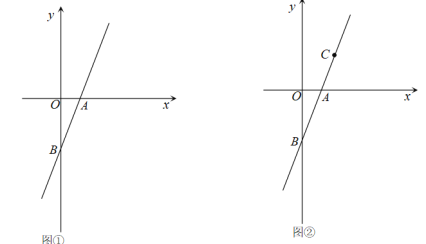
查看答案和解析>>【题目】已知,直线y=2x-2与x轴交于点A,与y轴交于点B.
(1)如图①,点A的坐标为_______,点B的坐标为_______;
(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.
①求点C的坐标;
②过动点P(m,0)且垂直与x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是_______;
(3)若∠ABN=45,求直线BN的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=

求:(1)反比例函数的解析式;
(2)点C的坐标;
(3)sin∠ABC的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程
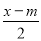 =x+
=x+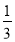 与
与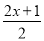 =6x﹣2的解互为倒数,
=6x﹣2的解互为倒数,(1)求m的值.
(2)若当y=m时,代数式ay3+by+1的值为5,求当y=﹣m时,代数式ay3+by+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2,4,6,8,…,排成如图:并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)设中间的数为x,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五位数,其它五位数的和能等于2015吗?如能,写出这五位数,如不能,说明理由.

相关试题

