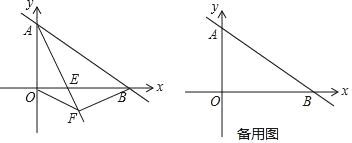
【题目】如图,已知一次函数y=﹣![]() x+6的图象与坐标轴交于A、B两点,AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B两点,AE平分∠BAO,交x轴于点E.
(1)求点B的坐标及直线AE的表达式;
(2)过点B作BF⊥AE,垂足为F,在y轴上有一点P,使线段PE+PF的值最小,求点P的坐标;
(3)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F,以EF为边作正方形EFMN,当点M落在坐标轴上时,求E点坐标.
参考答案:
【答案】(1)B(8,0),y=﹣2x+6;(2)P(0,﹣![]() );(3)点E坐标为(
);(3)点E坐标为(![]() ,0)或(6,0).
,0)或(6,0).
【解析】
(1)设OE=x,作EM⊥AB于M.在Rt△EBM中,根据EM2+BM2=EB2,可得x2+42=(8-x)2,求出x即可解决问题;
(2)如图2中,作点E关于y轴的对称点E′,连接FE′交y轴于P,此时PE+PF的值最小.想办法切线直线FE′的解析式即可解决问题;
(3)①如图3中,当点M在y轴上时,作FP⊥OB于P,FQ⊥OM于Q.利用全等三角形的性质,证明四边形OPFQ是正方形即可解决问题;②如图4中,当点M在x轴上时,易知OA=OE=6,可得E(6,0).
(1)如图1中,
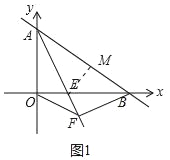
∵一次函数y=﹣![]() x+6的图象与坐标轴交于A、B点,
x+6的图象与坐标轴交于A、B点,
∴A(0,6),B(8,0),设OE=x,作EM⊥AB于M.
∵AE平分∠OAB,OE⊥OA,
∴OE=EM=x,
在△AEO和△AEM中,![]() ,
,
∴△AEO≌△AEM,
∴AM=AO=6,
∵OA=6,OB=8,∠AOB=90°,
∴AB=![]() =
=![]() =10,
=10,
∴BM=4,
在Rt△EBM中,∵EM2+BM2=EB2,
∴x2+42=(8﹣x)2,
∴x=3,
∴E(3,0),
设直线AE的解析式为y=kx+b,
则![]() ,
,
解得![]() ,
,
∴直线AE的解析式为y=﹣2x+6;
(2)如图2中,作点E关于y轴的对称点E′,连接FE′交y轴于P,此时PE+PF的值最小.
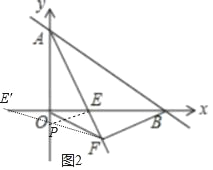
∵BF⊥AE,
∴直线BF的解析式为y=![]() x﹣4,
x﹣4,
由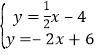 解得
解得![]() ,
,
∴F(4,﹣2),
∴直线FE′的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
∴P(0,﹣![]() ).
).
(3)①如图3中,当点M在y轴上时,作FP⊥OB于P,FQ⊥OM于Q.

∵四边形EFMN是正方形,
∴FE=FM,∠EFM=∠PFQ,
∴∠EFP=∠MFQ,
∵∠FPE=∠FQM=90°,
∴△FPE≌△FQM,
∴FP=FQ,四边形OPFQ是正方形,设边长为x.
∵∠AEO=∠BEF,∠AOE=∠PFE=90°,
∴∠FAQ=∠FBP,
∵∠AQF=∠BPF=90°,
∴△AQF≌△BPF,
∴AQ=BP,
∴6+x=8﹣x
∴x=1,
∴F(1,﹣1),
∴直线AF的解析式为y=﹣7x+6,
∴E(![]() ,0);
,0);
②如图4中,当点M在x轴上时,易知OA=OE=6,可得E(6,0).
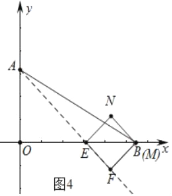
综上所述,满足条件的点E坐标为(![]() ,0)或(6,0).
,0)或(6,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费=自来水销售费用+污水处理费用)
自来水销售价格
污水处理价格
每户每月用水量
单价:元/吨
单价:元/吨
17吨及以下
a
0.80
超过17吨不超过30吨的部分
b
0.80
超过30吨的部分
6.00
0.80
已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求a,b的值.
(2)小王家6月份交水费184元,则小王家6月份用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD内一点P,AB=5,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP',则PP'的长为( )

A.2
B.
C.3
D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】运用“同一个图形的面积用不同方式表示”可以证明一类含有线段的等式,这种解决问题的方法我们称之为等面积法.学有所用:在等腰三角形ABC中,AB=AC,其一腰上的高BD=h,M是底边BC上的任意一点,M到腰AB的距离ME=h1,M到腰AC的距离MF=h2.
(1)请你结合图形1来证明:h1+h2=h;
(2)当点M在BC的延长线上时,h1、h2、h之间又有什么样的结论,请你在图2中画出图形;
(3)请利用以上结论解答下列问题,如图3,在平面直角坐标系中有两条直线l1:y=
 ,l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,求点M的坐标.
,l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.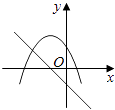
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若平行四边形ABCD的一个角的平分线把一条边分成长是4cm和5cm的两条线段,则平行四边形ABCD的周长是__________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从右边的二次函数y=ax2+bx+c图象中,观察得出了下面的五条信息:①a<0,②c=0,③函数的最小值为﹣3,④当x<0时,y>0,⑤当0<x1<x2<2时,y1>y2 , ⑥对称轴是直线x=2.你认为其中正确的个数为( )

A.2
B.3
C.4
D.5
相关试题

