【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
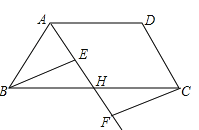
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是 ,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
参考答案:
【答案】(1)添加:EH=FH,证明见解析;(2)BH=EH,理由见解析.
【解析】
试题分析:(1)根据全等三角形的判定方法,可得出当EH=FH,BE∥CF,∠EBH=∠FCH时,都可以证明△BEH≌△CFH,
(2)由(1)可得出四边形BFCE是平行四边形,再根据对角线相等的平行四边形为矩形可得出BH=EH时,四边形BFCE是矩形.
试题解析:(1)添加:EH=FH,
证明:∵点H是BC的中点,
∴BH=CH,
在△BEH和△CFH中,
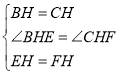 ,
,
∴△BEH≌△CFH(SAS);
(2)∵BH=CH,EH=FH,
∴四边形BFCE是平行四边形(对角线互相平分的四边形为平行四边形),
∵当BH=EH时,则BC=EF,
∴平行四边形BFCE为矩形(对角线相等的平行四边形为矩形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式因式分解:
(1)2m(a-b)-3n(b-a);
(2)16x2-64;
(3)-4a2+24a-36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列多项式分解因式.
(1)b2﹣b
(2)2xy﹣6y;
(3)a2﹣9b2;
(4)2x2﹣4x+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:x5·x7+x6·(-x3)2+2(x3)4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=
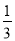 a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=
a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=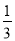 A1B2,….依次规律继续下去,则正方形AnBnCnDn的面积为 .
A1B2,….依次规律继续下去,则正方形AnBnCnDn的面积为 .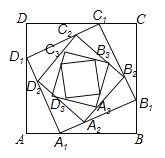
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:5x﹣3x=( )
A. 2x B. 2x2 C. ﹣2x D. ﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5a3b·(-3b)2+(-ab)(-6ab)2;
(2)(x-3y)2+(3y-x)(x+3y);
(3)x(x2+3)+x2(x-3)-3x(x2-x-1).
相关试题

