【题目】某校在一次大课间活动中,采用了四钟活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图. 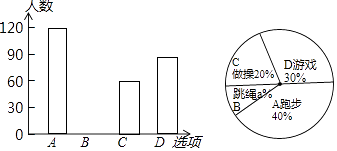
请结合统计图,回答下列问题:
(1)本次调查学生共人,a= , 并将条形图补充完整;
(2)如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?
(3)学校让每班在A、B、C、D四钟活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.
参考答案:
【答案】
(1)300;10;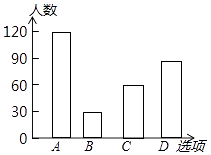
(2)解:2000×40%=800(人),
答:估计该校选择“跑步”这种活动的学生约有800人
(3)解:画树状图为:
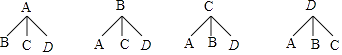
共有12种等可能的结果数,其中每班所抽到的两项方式恰好是“跑步”和“跳绳”的结果数为2,
所以每班所抽到的两项方式恰好是“跑步”和“跳绳”的概率= ![]() =
= ![]()
【解析】(1)120÷40%=300, a%=1﹣40%﹣30%﹣20%=10%,
∴a=10,
10%×300=30,
故答案为:300,10;图形如下:
(1)用A类学生数除以它所占的百分比即可得到总人数,再用1分别减去A、C、D类的百分比即可得到a的值,然后用a%乘以总人数得到B类人数,再补全条形统计图;(2)用2000乘以A类的百分比即可.(3)画树状图展示所有12种等可能的结果数,再找出每班所抽到的两项方式恰好是“跑步”和“跳绳”的结果数,然后根据概率公式求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体六个面分别标有字母A,B,C,D,E,F,其展开图如图所示,已知:A=x2-2xy,B=A-C,C=3xy+y2,若该正方体相对两个面上的多项式的和相等,试用x,y的代数式表示多项式D,并求当x=-1,y=-2时,多项式D的值.
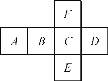
-
科目: 来源: 题型:
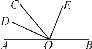
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,
(1)求∠BOC的度数;
(2)通过计算判断OE是否平分∠BOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,如果CD=
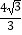 ,则AD= .
,则AD= . 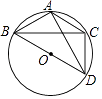
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探究函数y=x+
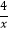 的图象与性质】
的图象与性质】
(1)函数y=x+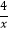 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下列四个函数图象中函数y=x+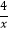 的图象大致是;
的图象大致是; 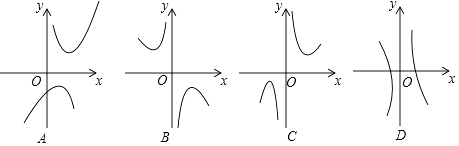
(3)对于函数y=x+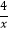 ,求当x>0时,y的取值范围. 请将下列的求解过程补充完整.
,求当x>0时,y的取值范围. 请将下列的求解过程补充完整.
解:∵x>0
∴y=x+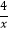 =(
=( 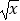 )2+(
)2+(  )2=(
)2=( 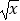 ﹣
﹣  )2+
)2+
∵(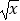 ﹣
﹣  )2≥0
)2≥0
∴y≥ .
(4)若函数y=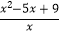 ,则y的取值范围 .
,则y的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,
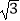 ).
).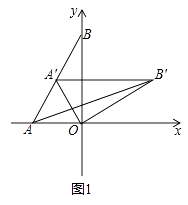
(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.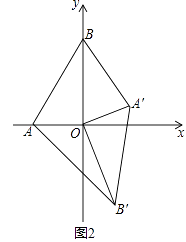
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解下列因式:
(1)
 . (2)
. (2)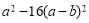 .
.
相关试题

