【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=4,D是BC上一个动点,连接AD,以AD为边向右侧作等腰直角△ADE,其中∠ADE=90°.
(1)如图2,G,H分别是边AB,BC的中点,连接DG,AH,EH.求证:△AGD∽△AHE;
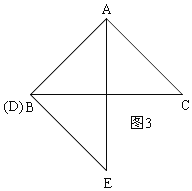
(2)如图3,连接BE,直接写出当BD为何值时,△ABE是等腰三角形;
(3)在点D从点B向点C运动过程中,求△ABE周长的最小值.

参考答案:
【答案】(1)证明见解析;(2)当BD=0或![]() 或
或![]() 时,△ABE是等腰三角形.;(3)△ABE周长最小值为
时,△ABE是等腰三角形.;(3)△ABE周长最小值为![]() .
.
【解析】(1)根据等腰直角三角形的性质和相似三角形的判定解答即可;
(2)分三种情况:
①当B与D重合时,即BD=0,如图3,此时AB=BE;
③当AB=AE时,如图4,此时E与C重合,可得BD的长;
③当AB=BE时,如图5,作辅助线,构建等腰直角三角形和全等三角形,证明△ADM≌△DEG,和△EMG是等腰直角三角形,则ME=![]() MG,根据(1)得:△AHD∽△AME,且
MG,根据(1)得:△AHD∽△AME,且![]() ,可计算BD的长;
,可计算BD的长;
(3)先确定△ABE周长的最小值时,E的位置:作点B关于直线MC的对称点N,连接AN交MC于点E′,此时△ABE′就是所求周长最小的△ABE;证明四边形ABMC是正方形,根据△ABD∽△AME,得∠AME=∠ABD=45°,知点E在射线MC上,利用勾股定理求AN的长,根据周长定义可得结论.
(1)证明:如图2,由题意知△ABC和△ADE都是等腰直角三角形,
∴∠B=∠DAE=45°.
∵H为BC中点,
∴AH⊥BC.
∴∠BAH=45°=∠DAE.
∴∠GAD=∠HAE.
在等腰直角△BAH和等腰直角△DAE中,
AH=![]() AB=
AB=![]() AG,AE=
AG,AE=![]() AD.
AD.
∴![]() ,
,
∴△AGD∽△AHE;
(2)解:分三种情况:
①当B与D重合时,即BD=0,如图3,此时AB=BE;
③当AB=AE时,如图4,此时E与C重合,
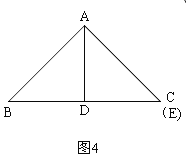
∴D是BC的中点,
∴BD=![]() BC=2
BC=2![]() ;
;
③当AB=BE时,如图5,过E作EH⊥AB于H,交BC于M,连接AM,过E作EG⊥BC于G,连接DH,
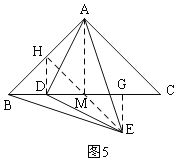
∵AE=BE,EH⊥AB,
∴AH=BH,
∴AM=BM,
∵∠ABC=45°,
∴AM⊥BC,△BMH是等腰直角三角形,
∵AD=DE,∠ADE=90°,
易得△ADM≌△DEG,
∴DM=EG,
∵∠EMG=∠BMH=45°,
∴△EMG是等腰直角三角形,
∴ME=![]() MG,
MG,
由(1)得:△AHD∽△AME,且![]() ,
,
∴∠AHD=∠AME=135°,ME=![]() DH,
DH,
∴∠BHD=45°,MG=DH,
∴△BDH是等腰直角三角形,
∴BD=DH=EG=DM=![]() ;
;
综上所述,当BD=0或![]() 或2
或2![]() 时,△ABE是等腰三角形;
时,△ABE是等腰三角形;
(3)解:当点D与点B重合时,点E的位置记为点M,连接CM,如图6,
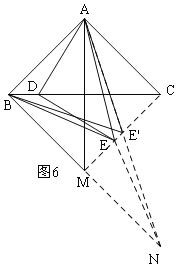
此时,∠ABM=∠BAC=90°,∠AMB=∠BAM=45°,BM=AB=AC.
∴四边形ABMC是正方形.
∴∠BMC=90°,
∴∠AMC=∠BMC-∠AMB=45°,
∵∠BAM=∠DAE=45°,
∴∠BAD=∠MAE,
在等腰直角△BAM和等腰直角△DAE中,
AM=![]() AB,AE=
AB,AE=![]() AD.
AD.
∴![]() .
.
∴△ABD∽△AME.
∴∠AME=∠ABD=45°
∴点E在射线MC上,
作点B关于直线MC的对称点N,连接AN交MC于点E′,
∵BE+AE=NE+AE≥AN=NE′+AE′=BE′+AE′,
∴△ABE′就是所求周长最小的△ABE.
在Rt△ABN中,
∵AB=4,BN=2BM=2AB=8,
∴AN=![]() .
.
∴△ABE周长最小值为AB+AN=4+4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
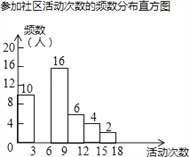
参加社区活动次数的频数、频率分布表
活动次数x
频数
频率
0<x≤3
10
0.20
3<x≤6
a
0.24
6<x≤9
16
0.32
9<x≤12
6
0.12
12<x≤15
m
b
15<x≤18
2
n
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
-
科目: 来源: 题型:
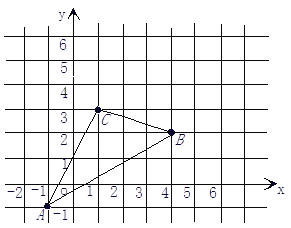
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)若把△ABC向上平移3个单位,再向右平移2个单位得△A'B'C',在 图 中 画 出 △ABC变化位置,并 写 出 A'、B'、C'的坐标。
(3)求出S△ABC
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是半径为1的半圆弧,△AOC为等边三角形,D是
是半径为1的半圆弧,△AOC为等边三角形,D是 上的一动点,则三角形AOD的面积S的取值范围是__________________
上的一动点,则三角形AOD的面积S的取值范围是__________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,中小学生每天在校体育活动时间不低于1h,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(h)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:

(1)此次抽查的学生为人;
(2)补全条形统计图;
(3)请你求出扇形统计图中B组扇形所对应的圆心角的度数
(4)若当天在校学生为1200人,请估计在当天达到国家规定体育活动时间的学生有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
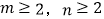 ,且
,且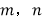 均为正整数,如果将
均为正整数,如果将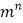 进行如下方式的“分解”,那么下列三个叙述:
进行如下方式的“分解”,那么下列三个叙述:(1)在
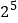 的“分解”中最大的数是13.
的“分解”中最大的数是13.(2)在
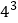 的“分解”中最小的数是13.
的“分解”中最小的数是13.(3)若
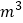 的“分解”中最小的数是23,则
的“分解”中最小的数是23,则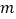 等于5.其中正确的是 .
等于5.其中正确的是 .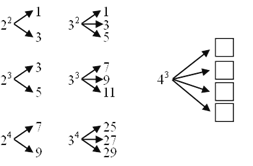
相关试题

