【题目】已知二次函数y=x2﹣(2k+1)x+k2+k(k>0)
(1)当k= ![]() 时,将这个二次函数的解析式写成顶点式;
时,将这个二次函数的解析式写成顶点式;
(2)求证:关于x的一元二次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根.
参考答案:
【答案】
(1)解:把k= ![]() 代入y=x2﹣(2k+1)x+k2+k(k>0)得y=x2﹣2x+
代入y=x2﹣(2k+1)x+k2+k(k>0)得y=x2﹣2x+ ![]() ,
,
因为y=(x﹣1)2﹣ ![]()
所以抛物线的顶点坐标为(1,﹣ ![]() )
)
(2)证明:△=(2k+1)2﹣4(k2+k)=1>0,
所以关于x的一元二次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根
【解析】(1)把k代入抛物线解析式,然后利用配方法可确定抛物线的顶点坐标;(2)计算判别式的值,然后判别式的意义进行证明.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面选项中符合代数式书写要求的是 ( )
A.
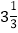 y2 B. ay·3 C.
y2 B. ay·3 C. 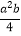 D. a×b+c
D. a×b+c -
科目: 来源: 题型:
查看答案和解析>>【题目】为控制禽流感病毒传播,某地关闭活禽交易市场,冷冻鸡肉销量上升,某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇,已知冷冻鸡肉在城市销售平均每箱的利润y1(百元)与销售数量x(箱)的关系为y1=
 在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=
在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=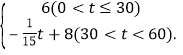
(1)t与x的关系是 ,将y2转换为x为自变量的函数,则y2= ;
(2)设春节期间售完全部冷冻鸡肉可获得总利润W(百元),当在城市销售量x(箱)的范围是0<x≤20时,求W与x的关系式(总利润=在城市销售利润+在乡镇销售利润);
(3)经测算,在20<x≤30的范围内,可以获得最大总利润,求这个最大总利润,并求出此时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学在沙滩上用石子摆成的小房子

观察图形的变化规律,则第10个小房子用了( )颗石子.
A. 119 B. 121 C. 140 D. 142
相关试题

