【题目】解答题。
(1)计算:(﹣1)2015+( ![]() )﹣3﹣(π﹣3.1)0
)﹣3﹣(π﹣3.1)0
(2)计算:(﹣2x2y)23xy÷(﹣6x2y)
(3)先化简,再求值:[(2x+y)2+(2x+y)(y﹣2x)﹣6y]÷2y,其中x=﹣ ![]() ,y=3.
,y=3.
(4)用整式乘法公式计算: ![]() .
.
参考答案:
【答案】
(1)解:(﹣1)2015+( ![]() )﹣3﹣(π﹣3.1)0
)﹣3﹣(π﹣3.1)0
=﹣1+ ![]() ﹣1
﹣1
=﹣1+27﹣1
=25;
(2)解:(﹣2x2y)23xy÷(﹣6x2y)
=4x4y23xy÷(﹣6x2y)
=12x5y3÷(﹣6x2y)
=﹣2x3y2
(3)解:[(2x+y)2+(2x+y)(y﹣2x)﹣6y]÷2y,
=(4x2+4xy+y2+y2﹣4x2﹣6y)÷2y
=(4xy+2y2﹣6y)÷2y
=2x+y﹣3
把x=﹣ ![]() ,y=3代入得:
,y=3代入得:
原式=2×(﹣ ![]() )+3﹣3=﹣1
)+3﹣3=﹣1
(4)解: ![]()
= ![]()
= ![]()
=620.
【解析】(1)直接利用有理数的乘方运算法则以及负整数指数幂的性质以及零指数幂的性质分别化简求出答案;(2)直接利用积的乘方运算法则结合整式乘除运算法则化简,求出答案;(3)首先利用乘法公式化简进而将已知数据代入求出答案;(4)直接利用平方差公式将原式变形进而求出答案.
【考点精析】认真审题,首先需要了解零指数幂法则(零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数)),还要掌握整数指数幂的运算性质(aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数))的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P以2cm/s的速度沿图1所示的边框从B→C→D→E→F→A的路径运动,记△ABP的面积为t(cm2),y与运动时间t(s)的关系如图2所示.
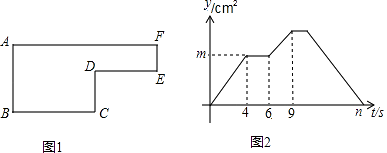
若AB=6cm,请回答下列问题:
(1)求图1中BC、CD的长及边框所围成图形的面积;
(2)求图2中m、n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,个位数比十位数字大4,而且这个两位数比它的数字之和的3倍大2,则这个两位数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2 , 直线l与l1、l2分别交于A、B两点,点M,N分别在l1、l2上,点M,N,P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
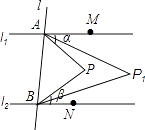
(1)当点P在l1与l2之间时. 求∠APB的大小(用含α、β的代数式表示);
(2)若∠APM的平分线与∠PBN的平分线交于点P1 , ∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 则∠AP1B= , ∠APnB= . (用含α、β的代数式表示,其中n为正整数)
(3)当点P不在l1与l2之间时. 若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数) -
科目: 来源: 题型:
查看答案和解析>>【题目】有3cm,3cm,6cm,6cm,12cm,12cm的六条线段,任选其中的三条线段组成一个等腰三角形,则最多能组成等腰三角形的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地的实际距离AB=5千米,画在地图上的距离为2厘米,则地图上的距离与实际距离的比为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 直线外一点与直线上各点连接的线段中,垂线最短 B. 点到直线的距离是这点到直线的垂线段
C. 过一点有且只有一条直线与已知直线平行 D. 在同一平面内,垂直于同一条直线的两直线平行
相关试题

