【题目】如图,抛物线![]() 与直线
与直线![]() 交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时,![]() ;
;
(3)是否存在点P,使△PAD是直角三角形,若存在,求出点P的坐标;若不存在,说明理由.

参考答案:
【答案】(1)y=x2+4x-1;(2)∴m=![]() ,-2,或-3时S四边形OBDC=2SS△BPD
,-2,或-3时S四边形OBDC=2SS△BPD
【解析】试题分析:(1)由x=0时带入y=x-1求出y的值求出B的坐标,当x=-3时,代入y=x-1求出y的值就可以求出A的坐标,由待定系数法就可以求出抛物线的解析式;
(2)连结OP,由P点的横坐标为m可以表示出P、D的坐标,可以表示出S四边形OBDC和2S△BPD建立方程求出其解即可.

(3)如图2,当∠APD=90°时,设出P点的坐标,就可以表示出D的坐标,由△APD∽△FCD就可与求出结论,如图3,当∠PAD=90°时,作AE⊥x轴于E,就有![]() ,可以表示出AD,再由△PAD∽△FEA由相似三角形的性质就可以求出结论.
,可以表示出AD,再由△PAD∽△FEA由相似三角形的性质就可以求出结论.
试题解析:
∵y=x-1,∴x=0时,y=-1,∴B(0,-1).
当x=-3时,y=-4,∴A(-3,-4).
∵y=x2+bx+c与直线y=x-1交于A、B两点,∴![]()
∴![]() ∴抛物线的解析式为:y=x2+4x-1;
∴抛物线的解析式为:y=x2+4x-1;
(2)∵P点横坐标是m(m<0),∴P(m,m2+4m-1),D(m,m-1)
如图1①,作BE⊥PC于E, ∴BE=-m.
CD=1-m,OB=1,OC=-m,CP=1-4m-m2,
∴PD=1-4m-m2-1+m=-3m-m2,
∴![]()
解得:m1=0(舍去),m2=-2,m3=![]()
如图1②,作BE⊥PC于E,
∴BE=-m.
PD=1-4m-m2+1-m=2-4m-m2,
![]()
解得:m=0(舍去)或m=-3,
∴m=![]() ,-2,或-3时S四边形OBDC=2S△BPD;
,-2,或-3时S四边形OBDC=2S△BPD;
)如图2,当∠APD=90°时,设P(a,a2+4a-1),则D(a,a-1),
∴AP=m+4,CD=1-m,OC=-m,CP=1-4m-m2,
∴DP=1-4m-m2-1+m=-3m-m2.
在y=x-1中,当y=0时,x=1,
∴(1,0),
∴OF=1,∴CF=1-m.AF=4![]()
∵PC⊥x轴,
∴∠PCF=90°,
∴∠PCF=∠APD,
∴CF∥AP,
∴△APD∽△FCD,
![]() ∴
∴![]()
解得:m=1舍去或m=-2,∴P(-2,-5)
如图3,当∠PAD=90°时,作AE⊥x轴于E,
∴∠AEF=90°.CE=-3-m,EF=4,AF=4![]()
PD=1-m-(1-4m-m2)=3m+m2.
∵PC⊥x轴,∵PC⊥x轴,
∴∠DCF=90°,
∴∠DCF=∠AEF,
∴AE∥CD.
![]()
∴AD=![]() (-3-m)
(-3-m)
∵△PAD∽△FEA,
∴![]()
![]()
∴m=-2或m=-3
∴P(-2,-5)或(-3,-4)与点A重合,舍去,
∴P(-2,-5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式
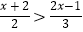 并把解集在数轴上表示出来.
并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )
A.(a+b)元
B.(3a+2b)元
C.(2a+3b)元
D.5(a+b)元 -
科目: 来源: 题型:
查看答案和解析>>【题目】若m、n是一元二次方程x2﹣5x+2=0的两个实数根,则m+n﹣mn的值是( )
A.7
B.﹣7
C.3
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,
 ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A. (
 ,
, ) B. (
) B. ( ,
, ) C. (
) C. ( ,
, ) D. (
) D. ( ,4
,4 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了增强学生的安全意识,组织全校学生參加安全知识竞赛,赛后组委会随机抽查部分学生的成绩进行统计(由高到低分四个等级).根据调査的数据绘制成如下的条形统计图和扇形统计图.

根据以上不完整的统计图提供的信息,解答下列问题:
(1)组委会共抽査了名学生的安全知识竞赛成绩,扇形统计图中B级所占的百分比 b=扇形统计图中.C级所对应的圆心角的度数是度.
(2)补全条形统计图:
(3)若该校共有800名学生,请估算该校安全知识竞赛成绩获得A级的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD丄AC 于D,EF丄AC 于F.∠AMD=∠AGF.∠1=∠2=35°

(1)求∠GFC的度数:
(2)求证:DM∥BC.
相关试题

