【题目】解不等式 并把解集在数轴上表示出来．

参考答案：

【答案】解：去分母，去括号得，3x+6＞4x﹣2，
合并同类项得，﹣x＞﹣8，
系数化为1得，x＜8，
这个不等式解集在数轴上表示如下：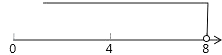

【解析】利用不等式的基本性质，先去分母、再去括号、移项、合并同类项即可．
【考点精析】利用不等式的解集在数轴上的表示和一元一次不等式的解法对题目进行判断即可得到答案，需要熟知不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈；步骤：①去分母；②去括号；③移项；④合并同类项； ⑤系数化为1（特别要注意不等号方向改变的问题）．

关闭