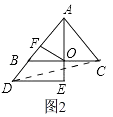
【题目】已知,如图①,△ABC、△AED是两个全等的等腰直角三角形(其顶点B、E重合),∠BAC=∠AED=90°,O为BC的中点,F为AD的中点,连接OF.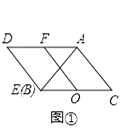
(1)问题发现
①如图①,线段OF与EC的数量关系为;
②将△AED绕点A逆时针旋转45°,如图②,OF与EC的数量关系为;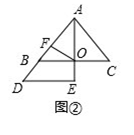
(2)类比延伸
将图①中△AED绕点A逆时针旋转到如图③所示的位置,请判断线段OF与EC的数量关系,并给出证明.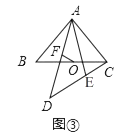
(3)拓展探究
将图①中△AED绕点A逆时针旋转,旋转角为α,0°≤α≤90°,AD= ![]() ,△AED在旋转过程中,存在△ACD为直角三角形,请直接写出线段CD的长.
,△AED在旋转过程中,存在△ACD为直角三角形,请直接写出线段CD的长.
参考答案:
【答案】
(1)OF= ![]() EC;OF=
EC;OF= ![]() EC
EC
(2)
解:OF= ![]() EC.
EC.
证明:在等腰直角△ADE中,F为AD的中点,
∴AF= ![]() AD=
AD= ![]() AE,
AE,
在等腰直角△ABC中,O为BC的中点,
如图1,
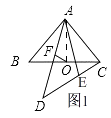
连接AO,
∴AO= ![]() AC,∠BAO=∠CAO=45°,
AC,∠BAO=∠CAO=45°,
∵∠DAE=45°,
∴∠DAE=∠CAO,
∴∠DAE﹣∠EAO=∠CAO﹣∠EAO,
即∠DAO=∠CAE,
∵AE=AC,
∴AF=AO,
∴ ![]() =
= ![]() ,
,
∴△AFO∽△AEC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴OF= ![]() EC,
EC,
(3)
解:∵△ABC和△AED是两个全等的等腰直角三角形,
∴AD=BC= ![]() ,
,
∴ED=AE=AB=AC=1,
△ACD为直角三角形时,分两种情况:
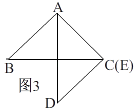
①当AD与AB重合时,如图2,
连接CD,
∵△ACD为直角三角形,AD⊥AC,
即将△ADE逆时针旋转45°,
∵AD= ![]() ,AC=1,
,AC=1,
∴由勾股定理可得CD= ![]() =
= ![]() ;
;
②当AE与AC重合时,如图3,
△ACD为直角三角形,AC⊥CD,
即将△ADE逆时针旋转90°,此时CD=AC=1.
即:CD的长为 ![]() 或1.
或1.
【解析】解:(1)①∵△ABC、△AED是两个全等的等腰直角三角形,
∴AD=BC,
∵O为BC的中点,F为AD的中点,
∴AF=OC,
∵∠BAC=∠AED=90°,
∴AD∥BC,
∴四边形AFOC是平行四边形,
∴OF=AC= ![]() EC,
EC,
故答案:OF= ![]() EC;②如图,
EC;②如图,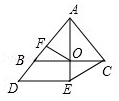
∵AO= ![]() AC,∠BAO=∠CAO=45°,
AC,∠BAO=∠CAO=45°,
∵∠DAE=45°,
∴∠DAE=∠CAO,
∴∠DAE﹣∠EAO=∠CAO﹣∠EAO,
即∠DAO=∠CAE,
∵AE=AC,
∴AF=AO,
∴ ![]() =
= ![]() ,
,
∴△AFO∽△AEC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴OF= ![]() EC,
EC,
故答案OF= ![]() EC
EC
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某品牌电风扇销售量的情况,对某商场5月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该商场5月份售出这种品牌的电风扇共多少台?
(2)若该商场计划订购这三种型号的电风扇共2000台,根据5月份销售量的情况,求该商场应订购丙种型号电风扇多少台比较合理?

-
科目: 来源: 题型:
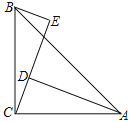
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D、E
(1) 求证:CD=BE
(2) 若AD=3.5 cm,DE=2.7 cm,求BE的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,E为AC上一点,∠ABE=∠AEB,∠CDE=∠CED.
求证:BE⊥DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F
(1) 说明BE=CF的理由
(2) 如果AB=a,AC=b,求AE、BE的长

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点,若一个多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
(1)求出图中格点四边形DEFG对应的S,N,L.
(2)已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,若某格点多边形对应的N=82,L=38,求S的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)、B(3,0)两点,与y轴交于点C(0,3).
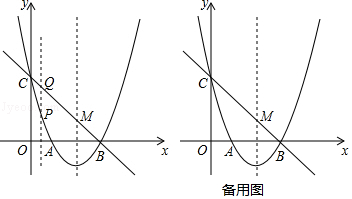
(1)求抛物线的解析式;
(2)设点P是位于直线BC下方的抛物线上一动点,过点P作y轴的平行线交直线BC于点Q,求线段PQ的最大值;
(3)在(2)的条件下,抛物线的对称轴与直线BC交于点M,问是否存在点P,使以M、P、Q为顶点的三角形与△CBO相似?若存在,请求出点P的坐标;若不存在,请说明理由.
相关试题

