搜索
【题目】已知：
是最小的正整数，且
、满足
，请回答问题：
（1）请直接写出、、
的值．
，
，
．
（2）、、所对应的点分别为
、
、
，点
为一动点，其对应的数为
，点在、之间运动时，请化简式子：
（请写出化简过程）
（3）在（1）（2）的条件下，点、、开始在数轴上运动，若点以每秒
个单位长度的速度向左运动，同时，点和点分别以每秒
个单位长度和
个单位长度的速度向右运动，假设经过
秒钟过后，若点与点之间的距离表示为
，点与点之间的距离表示为
．请问：
的值是否随着时间的变化而改变？若变化，请说明理由：若不变，请求其值．
参考答案：
【答案】（1）-1,1,6；（2）-10；（3）不变，值为3．
【解析】
(1)根据最小的正整数是1，推出b=1，再利用非负数的性质求出a、c即可．
(2)首先确定x的范围，再化简绝对值即可．
(3)BCAB的值不变．根据题意用n，t表示出BC、AB即可解决问题．
解：∵b是最小的正整数，
∴b=1，
∵(c6)2+|a+b|=0，(c6)20，|a+b|0，
∴c=6，a=1，b=1，
故答案为1，1，6;
（2）．由题意1<x<1，
∴|x+1||x1|2|x+5|＝x+1+x12x10＝10．
（3）不变，
由题意BC＝5+5nt2nt＝5+3nt，AB＝nt+2+2nt＝2+3nt，
∴BCAB＝(5+3nt)(2+3nt)＝3，
∴BCAB的值不变，BCAB＝3．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校七年级共有800名学生，准备调查他们对“低碳”知识的了解程度．
（1）在确定调查方式时，团委设计了以下三种方案：
方案一：调查七年级部分女生；
方案二：调查七年级部分男生；
方案三：到七年级每个班去随机调查一定数量的学生．
请问其中最具有代表性的一个方案是 ；
（2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图（如图①、图②所示），请你根据图中信息，将两个统计图补充完整；
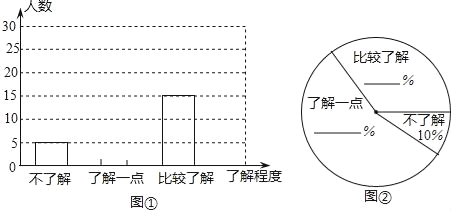
（3）在扇形统计图中，“比较了解”所在扇形的圆心角的度数是 ．
（4）请你估计该校七年级约有 名学生比较了解“低碳”知识．
-
科目： 来源： 题型：
查看答案和解析>>【题目】再读教材:
宽与长的比是
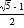(约为0.618)的矩形叫做黄金矩形，黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计，下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步，如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处，
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形，
问题解决:
（1）图③中AB=________(保留根号);
（2）如图③,判断四边形 BADQ的形状,并说明理由;
（3）请写出图④中所有的黄金矩形,并选择其中一个说明理由.
（4）结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，数轴上线段AB＝2(单位长度)，线段CD＝4(单位长度)，点A在数轴上表示的数是－10，点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动，同时线段CD以每秒2个单位长度的速度向左匀速运动．设运动时间为t s.
(1)当点B与点C相遇时，点A、点D在数轴上表示的数分别为________；
(2)当t为何值时，点B刚好与线段CD的中点重合；
(3)当运动到BC＝8(单位长度)时，求出此时点B在数轴上表示的数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题：①因为
，所以是
；②平行于同一条直线的两条直线平行；③相等的角是对顶角；④三角形三条中线的交点是三角形的重心；⑤同位角相等．其中真命题的个数是（ ）A.1B.2C.3D.4
-
科目： 来源： 题型：
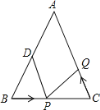
查看答案和解析>>【题目】△ABC中，AB=AC=12厘米，∠B=∠C，BC=8厘米，点D为AB的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．若点Q的运动速度为_____厘米/秒，△BPD与△CQP全等.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点B，F，C，E在同一直线上，AC，DF相交于点G，且△ABC≌△DEF
(1)若△ABC的周长为12cm，AB=3cm，BC=4cm，求DF的长.
(2)若DE⊥BC与点E，∠A＝65°，求∠AGF的度数.
相关试题
