【题目】如图,点B,F,C,E在同一直线上,AC,DF相交于点G,且△ABC≌△DEF
(1)若△ABC的周长为12cm,AB=3cm,BC=4cm,求DF的长.
(2)若DE⊥BC与点E,∠A=65°,求∠AGF的度数.

参考答案:
【答案】(1)5;(2)50°.
【解析】
(1)由全等三角形性质,得DE=AB=3,EF=BC=4,即可求得DF的长度;
(2)由全等三角形性质,则∠D=∠A=65°,∠DFE=∠ACB=25°,有外角性质,得到∠AGF的度数.
解:(1)∵△ABC≌△DEF,
∴DE=AB=3,EF=BC=4,
∴DF=12-3-4=5;
(2)∵△ABC≌△DEF,
∴∠D=∠A=65°,∠DFE=∠ACB,
∵DE⊥BC,
∴∠E=90°,
∴∠DFE=180°-90°-65°=25°,
∴∠DFE=∠ACB=25°,
∴∠AGF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
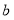 是最小的正整数,且
是最小的正整数,且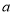 、
、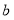 满足
满足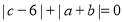 ,请回答问题:
,请回答问题:(1)请直接写出
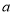 、
、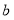 、
、 的值.
的值.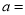 ,
, ,
, .
.(2)
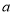 、
、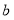 、
、 所对应的点分别为
所对应的点分别为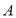 、
、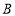 、
、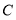 ,点
,点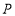 为一动点,其对应的数为
为一动点,其对应的数为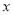 ,点
,点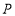 在
在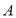 、
、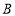 之间运动时,请化简式子:
之间运动时,请化简式子: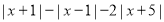 (请写出化简过程)
(请写出化简过程)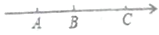
(3)在(1)(2)的条件下,点
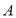 、
、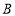 、
、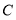 开始在数轴上运动,若点
开始在数轴上运动,若点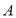 以每秒
以每秒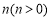 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点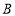 和点
和点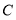 分别以每秒
分别以每秒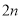 个单位长度和
个单位长度和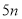 个单位长度的速度向右运动,假设经过
个单位长度的速度向右运动,假设经过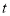 秒钟过后,若点
秒钟过后,若点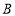 与点
与点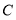 之间的距离表示为
之间的距离表示为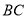 ,点
,点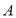 与点
与点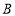 之间的距离表示为
之间的距离表示为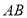 .请问:
.请问: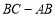 的值是否随着时间的变化而改变?若变化,请说明理由:若不变,请求其值.
的值是否随着时间的变化而改变?若变化,请说明理由:若不变,请求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①因为
 ,所以是
,所以是 ;②平行于同一条直线的两条直线平行;③相等的角是对顶角;④三角形三条中线的交点是三角形的重心;⑤同位角相等.其中真命题的个数是( )
;②平行于同一条直线的两条直线平行;③相等的角是对顶角;④三角形三条中线的交点是三角形的重心;⑤同位角相等.其中真命题的个数是( )A.1B.2C.3D.4
-
科目: 来源: 题型:
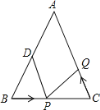
查看答案和解析>>【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为_____厘米/秒,△BPD与△CQP全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,D为CB上一点,过点D作DE⊥AB于点E.
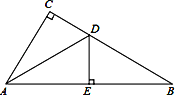
(1)若CD=DE,判断∠CAD与∠BAD的数量关系;
(2)若AE=EB,CB=10,AC=5,求△ACD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( )

A. 鸡 20 只,兔 15 只 B. 鸡 12 只,兔 23 只
C. 鸡 15 只,兔 20 只 D. 鸡 23 只,兔 12 只
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,AD平分∠BAC,BD=CD

(1)求证:BE=CF;
(2)已知AC=10,DE=4,BE=2,求△AEC的面积
相关试题

