Question

【题目】（1）问题发现

如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE，求∠AEB的度数．

（2）拓展探究

如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．请求∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．

Answer 1

【答案】（1）60°；（2）∠AEB=90°AE= BE+2CM．

【解析】解：（1）∵△ACB和△DCE均为等边三角形，

∴CA=CB，CD=CE，∠ACB=∠DCE=60°，

∴∠ACD=60°﹣∠DCB =∠BCE．

在△ACD和△BCE中，

，

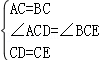∴△ACD≌△BCE（SAS）．

∴∠ADC=∠BEC．

∵△DCE为等边三角形，

∴∠CDE=∠CED=60°．

∵点A，D，E在同一直线上，

∴∠ADC=120°，

∴∠BEC=120°．

∴∠AEB=∠BEC﹣∠CED=60°．

（2）

∵△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°

∴CA=CB，CD=CE．

且∠ACD=∠BCE．

在△ACD和△BCE中，

，

∴△ACD≌△BCE（SAS）．

∴AD=BE，∠ADC=∠BEC．

∵△DCE为等腰直角三角形，

∴∠CDE=∠CED=45°．

∵点A，D，E在同一直线上，

∴∠ADC=135°，

∴∠BEC=135°．

∴∠AEB=∠BEC﹣∠CED=90°．

∵CD=CE，CM⊥DE，

∴DM=ME．

∵∠DCE=90°，

∴DM=ME=CM．

∴AE=AD+DE=BE+2CM．