【题目】如图,△ABC中AB=AC , ∠C=30°,AB的垂直平分线MN分别交BC、AB于点M、N , 试探究BM与CM之间的数量关系. 
参考答案:
【答案】解:连接AM , ∵AB=BC , ∠C=30°, ∴∠B=30°,∵AB的垂直平分线是MN,∴∠MAC=90°,CM=2AM,∴AB=2BM,∴CM=2BM,
【解析】连接AM,∵AB=BC , ∠C=30°∴∠B=30°, ∵AB的垂直平分线是MN,,∴∠MAC=90°,CM=2AM, ∴AB=2BM,,∴CM=2BM.
【考点精析】通过灵活运用线段垂直平分线的性质和等腰三角形的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a-3|+(b+4)2=0,则(a+b)2003=___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(0,-2)向上平移2个单位后的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A. 有两边和一角相等的两个三角形全等 B. 有一角相等的两个等腰三角形全等
C. 有一边相等的两个等腰直角三角形全等 D. 有一边相等的两个等边三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3x﹣2x=1
B.﹣2x﹣2=﹣ ?
?
C.(﹣a)2?a3=a6
D.(﹣a2)3=﹣a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠3=75°,那么∠4的度数是( )
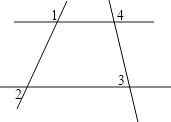
A.75°
B.45°
C.105°
D.135°
相关试题

