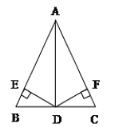
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
(1)图中共有_________对全等三角形.
(2)求证:AD是△ABC的角平分线.
参考答案:
【答案】(1)3,(2)见详解
【解析】
(1)根据条件D为BC中点可得BD=CD,再有条件BE=CF,可利用HL证明;Rt△BED≌Rt△CFD,进而得到∠B=∠C,从而得到DE=DF,AB=AC,可用HL证明△ABD≌△ACD,又可得到AE=AF,再利用SSS可证明△AED≌△AFD;
(2)根据全等三角形的判定与性质即可求解.
(1)3对,分别是△BED≌△CFD,△ABD≌△ACD,△AED≌△AFD;
故填:3;
(2)证明:根据题意可知:
BD=CD,BE=CF,
![]() Rt△DBE≌Rt△DCF(HL),
Rt△DBE≌Rt△DCF(HL),
![]() DE=DF
DE=DF
在Rt△ADE和Rt△ADF中
![]()
![]() Rt△ADE≌Rt△ADF(HL),
Rt△ADE≌Rt△ADF(HL),
![]()
![]()
即AD是△ABC的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线l1与x轴、y轴分别交于点A(3,0)、B(0,2).
(1)如图2,点M是AB的中点,过点M作ME⊥x轴,MF⊥y轴,垂足分别为E、F.则点M 的坐标为 ;
(2)如图3,直线l2经过点B,且与l1互相垂直,过点C(0,﹣1)作CD⊥y轴,交l2于点D.则以直线l2为图像的函数表达式为 ;
(3)图1中,在x轴上是否存在点P,使得△APB是等腰三角形.如果存在,请求出点P的坐标;如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ΔABC中,AD是高,AE、BF是角平分线,它们相交与点O,∠BAC=50°,∠C=70°,则∠DAC的度数为__________,∠BOA的度数为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.F是OC上另一点,连接DF,EF.求证:DF=EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】生活中,有人喜欢把传送的便条折成“
 ”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为
”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为 厘米,分别回答下列问题:
厘米,分别回答下列问题:
 如果长方形纸条的宽为
如果长方形纸条的宽为 厘米,并且开始折叠时起点
厘米,并且开始折叠时起点 与点
与点 的距离为
的距离为 厘米,那么在图②中,
厘米,那么在图②中, ________厘米;在图④中,
________厘米;在图④中, ________厘米.
________厘米. 如果长方形纸条的宽为
如果长方形纸条的宽为 厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点
厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点
的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点 与点
与点 的距离(结果用
的距离(结果用 表示).
表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与双曲线
与双曲线 相交于
相交于 、
、 两点,过点
两点,过点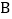 作
作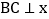 轴于点
轴于点 ,连接
,连接 ,则
,则 的面积为( )
的面积为( )
A. 3 B. 1.5 C. 4.5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】“丰收1号”小麦的试验田是边长为
 米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(
米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为( )米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
)米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
相关试题

