【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,则
,则![]() 的面积为( )
的面积为( )

A. 3 B. 1.5 C. 4.5 D. 6
参考答案:
【答案】A
【解析】
因为直线与双曲线的交点坐标就是直线解析式与双曲线的解析式联立而成的方程组的解,故求出直线解析式与双曲线的解析式,然后将其联立解方程组,得点B与C的坐标,再根据三角形的面积公式及坐标的意义求解.
∵直线y=mx(m≠0)与双曲线y=nx1相交于A(1,3),
∴m=3,![]() =3,
=3,
∴m=3,n=3,
∴直线的解析式为:y=3x,双曲线的解析式为:y=![]() ,
,
解方程组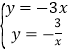 ,得:
,得:![]() ,
,![]() ,
,
则点A的坐标为(1,3),点B的坐标为(1,3),
∴点C的坐标为(1,0),
∴S△ABC=![]() ×1×(3+3)=3.
×1×(3+3)=3.
故答案选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.F是OC上另一点,连接DF,EF.求证:DF=EF.

-
科目: 来源: 题型:
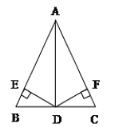
查看答案和解析>>【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
(1)图中共有_________对全等三角形.
(2)求证:AD是△ABC的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活中,有人喜欢把传送的便条折成“
 ”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为
”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为 厘米,分别回答下列问题:
厘米,分别回答下列问题:
 如果长方形纸条的宽为
如果长方形纸条的宽为 厘米,并且开始折叠时起点
厘米,并且开始折叠时起点 与点
与点 的距离为
的距离为 厘米,那么在图②中,
厘米,那么在图②中, ________厘米;在图④中,
________厘米;在图④中, ________厘米.
________厘米. 如果长方形纸条的宽为
如果长方形纸条的宽为 厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点
厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点
的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点 与点
与点 的距离(结果用
的距离(结果用 表示).
表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】“丰收1号”小麦的试验田是边长为
 米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(
米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为( )米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
)米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
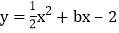 与
与 轴交于
轴交于 、
、 两点,与
两点,与 交于
交于 点,且
点,且 ,点
,点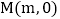 是
是 轴上的一个动点,当
轴上的一个动点,当 的值最小时,
的值最小时, 的值是( )
的值是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为24的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是( )

A. 12B. 6C. 3D. 1
相关试题

