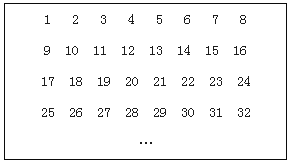
【题目】把正整数1,2,3,4,…,排列成如图(1)所示的一个表,从上到下分别称为第1行、第2行、…,从左到右分别称为第1列、第2列、….用图(2)所示的方框在图1中框住16个数,把其中没有被阴影覆盖的四个数分别记为![]() 、
、![]() 、
、![]() 、
、![]() . 设
. 设![]() =
=![]() .
.

(1) (2)
(1)在图(1)中,2017排在第_________行第_________列;
(2)![]() 的值是否为定值?如果是,请求出它的值;如果不是,请说明理由;
的值是否为定值?如果是,请求出它的值;如果不是,请说明理由;
(3)将图(1)中的奇数都改为原数的相反数,偶数不变.
①设此时图(1)中排在第![]() 行第
行第![]() 列的数(
列的数(![]() 、
、![]() 都是正整数)为
都是正整数)为![]() ,请用含
,请用含![]() 、
、![]() 的式子表示
的式子表示![]() ;
;
②此时![]() 的值能否为3918?如果能,请求出
的值能否为3918?如果能,请求出![]() 所表示的数;如果不能,请说明理由.
所表示的数;如果不能,请说明理由.
参考答案:
【答案】 253 1
【解析】试题分析:(1)由题意知8个数为一行,每一行的第一个数是8的(行数-1)+1,后面的数依次加1,由此规律可判断2017所在的位置;
(2)根据图表,用含有x的代数式分别表示A、B、C、D,即可得出结论;
(3)①分两种情况进行讨论即可求解;
②不能,A在第121行,第6列.此时图(2)的方框只能框到3列数, ![]() 、
、![]() 都框不到数了,所以
都框不到数了,所以![]() 的值不能为3918.
的值不能为3918.
试题解析:(1)2017÷8=252┈┈1,
故2017在第253行,第1列;
(2)是定值,由题知:A-B+C-D=x-(x+24)+x+27-(x+3)= x-x-24+x+27-x-3=0,因此A-B+C-D的值为定值,这个定值为0.
(3)①法一:当n是奇数时, ![]()
![]()
![]() ;
;
当n是偶数时, ![]()
![]()
![]() .
.
法二: ![]()
![]() ·
·![]() .
.
②不能,理由如下:如果结果等于3918,说明此时![]() 、
、![]() 都是正数,
都是正数, ![]() 、
、![]() 都是负数.因为
都是负数.因为![]() =
=![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() .
.
所以![]()
![]()
![]()
![]() =3918,解得
=3918,解得![]() ,因此
,因此![]() 所表示的数应为966.
所表示的数应为966.
因为966=8×120+6,
∴此时A在第121行,第6列.此时图(2)的方框只能框到3列数, ![]() 、
、![]() 都框不到数了,所以
都框不到数了,所以![]() 的值不能为3918..
的值不能为3918..
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△A′B′C′,且相似比为2∶3,则对应边上的高的比等于( )
A. 2∶3 B. 3∶2 C. 4∶9 D. 9∶4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-2,n)在抛物线
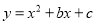 上.
上.(1)若b=1,c=3,①求n的值;
②求出此时二次函数在
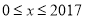 上的最小值
上的最小值(2)若此抛物线经过点B(6,n),且二次函数
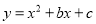 的最小值是-4,请画出点P(
的最小值是-4,请画出点P(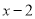 ,
, 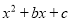 )的纵坐标随横坐标变化的图象,并说明理由.
)的纵坐标随横坐标变化的图象,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣2向左平移1个单位后所得抛物线的表达式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣3+(﹣5)的结果是( )
A.﹣2
B.﹣8
C.8
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动﹣旋转变换
(1)如图①,在△ABC中,∠ABC=130°,将△ABC绕点C逆时针旋转50°得到△A′B′C,连接BB′,求∠A′B′B的大小;
(2)如图②,在△ABC中,∠ABC=150°,AB=3,BC=5,将△ABC绕点C逆时针旋转60°得到△A′B′C,连接BB′,以A′为圆心,A′B′长为半径作圆.
(Ⅰ)猜想:直线BB′与⊙A′的位置关系,并证明你的结论;
(Ⅱ)连接A′B,求线段A′B的长度;
(3)如图③,在△ABC中,∠ABC=α(90°<α<180°),AB=m,BC=n,将△ABC绕点C逆时针旋转2β角度(0°<2β<180°)得到△A′B′C,连接A′B和BB′,以A′为圆心,A′B′长为半径作圆,问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由,并求此条件下线段A′B的长度(结果用角α或角β的三角函数及字母m、n所组成的式子表示)
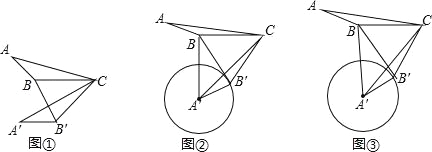
-
科目: 来源: 题型:
查看答案和解析>>【题目】用同一种规格的下列多边形瓷砖不能镶嵌成平面图案的是( )
A.三角形B.正方形C.正五边形D.正六边形
相关试题

