搜索
【题目】如图，一次函数
（k≠0）和反比例函数
（m≠0）的图象交于点A（﹣1，6），B（a，﹣2）．
（1）求一次函数与反比例函数的解析式；
（2）根据图象直接写出
时，x的取值范围．
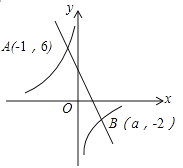
参考答案：
【答案】（1）
，
；（2）x＜﹣1或0＜x＜3．
【解析】
试题分析：（1）把点A坐标代入反比例函数求出k的值，也就求出了反比例函数解析式，再把点B的坐标代入反比例函数解析式求出a的值，得到点B的坐标，然后利用待定系数法即可求出一次函数解析式；
（2）找出直线在一次函数图形的上方的自变量x的取值即可．
试题解析：（1）把点A（﹣1，6）代入反比例函数
（m≠0）得：m=﹣1×6=﹣6，∴．
将B（a，﹣2）代入得：
，a=3，∴B（3，﹣2），将A（﹣1，6），B（3，﹣2）代入一次函数y1=kx+b得：
，∴
，∴；
（2）由函数图象可得：x＜﹣1或0＜x＜3．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知y是x的函数，自变量x的取值范围x＞0，下表是y与x的几组对应值
小腾根据学校函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．
下面是小腾的探究过程，请补充完整：
（1）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（2）根据画出的函数图象，写出：
①x＝4对应的函数值y约为 ；
②该函数的一条性质： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，过点A（－6，0）的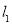直线
与直线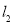
；y=2x相交于点B（m，4）．（1）求直线
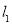的表达式；（2）过动点P（n，0）且垂于x轴的直线与
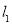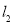，的交点分别为C，D，当点C位于点D上方时，写出n的取值范围．
-
科目： 来源： 题型：
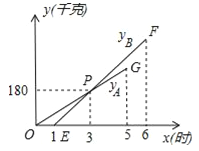
查看答案和解析>>【题目】某物流公司引进A、B两种机器人用来搬运某种货物，这两种机器人充满电后可以连续搬运5小时，A种机器人于某日0时开始搬运，过了1小时，B种机器人也开始搬运，如图，线段OG表示A种机器人的搬运量yA（千克）与时间x（时）的函数图象，根据图象提供的信息，解答下列问题：
（1）求yB关于x的函数解析式；
（2）如果A、B两种机器人连续搬运5个小时，那么B种机器人比A种机器人多搬运了多少千克？
-
科目： 来源： 题型：
查看答案和解析>>【题目】一家商店将某种服装按成本提高40%标价，又以8折优惠卖出，结果每件服装仍可获利15元，则这种服装每件的成本价是元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】温州市2019年一季度生产总值（GDP）为129 800 000 000元．将129 800 000 000用科学记数法表示应为（ ）
A. 1298×108B. 1.298×108C. 1.298×1011D. 1.298×1012
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4
B.3,4,5
C.3,4,6
D.3,4,7
相关试题
