搜索
【题目】已知双曲线：
与抛物线：y=ax2+bx+c交于A（2，3）、B（m，2）、C（﹣3，n）三点．
（1）求双曲线与抛物线的解析式；
（2）在平面直角坐标系中描出点A、点B、点C，并求出△ABC的面积．
参考答案：
【答案】（1）y=
，y=﹣
x2+
x+3；（2）5.
【解析】分析：（1）函数图象过某一点时，这点就满足关系式，利用待定系数法分别求出反比例函数与二次函数解析式即可；
（2）根据A，B，C三点的坐标可以得出△ADB，△BCE和梯形ADEC的面积，用梯形面积减去两三角形面积即可得到△ABC的面积．
详解：（1）把点A（2，3）代入
得：k=6，
∴y=，
把B（m，2）、C（﹣3，n）分别代入y=得，
m=3，n=﹣2，
把A（2，3）、B（3，2）、C（﹣3，﹣2）分别代入y=ax2+bx+c得：
，
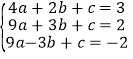解得：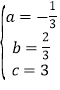
，
∴抛物线的解析式为：y=﹣x2+x+3；
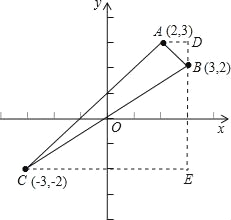
（2）描点画图得：
S△ABC=S梯形ADEC﹣S△ADB﹣S△BCE，
=
（1+6）×5﹣×1×1﹣×6×4，
=
﹣﹣12，
=5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探索规律：将连续的偶2，4，6，8，…，排成如表：
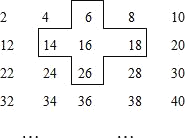
（1）请你求出十字框中的五个数的和；
（2）设中间的数为x，请你用含x的式子表示十字框中的五个数的和；
（3）若将十字框上下左右移动，可框住另外的五个数，这五个数的和能等于2018吗？如能，写出这五个数，如不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】知识链接：
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法，通过“转化、化归”通常可以实现化未知为已知，化复杂为简单，从而使问题得以解决.
（1）问题背景：已知：△ABC.试说明：∠A+∠B+∠C=180°.
问题解决：（填出依据）
解：（1）如图①，延长AB到E，过点B作BF∥AC.
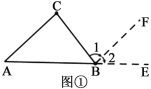
∵BF∥AC（作图）
∴∠1=∠C（ ）
∠2=∠A（ ）
∵∠2+∠ABC+∠1=180°（平角的定义）
∴∠A+∠ABC+∠C=180°（等量代换）
小结反思：本题通过添加适当的辅助线，把三角形的三个角之和转化成了一个平角，利用平角的定义，说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
（2）类比探究：请同学们参考图②，模仿（1）的解决过程试说明“三角形的三个内角和等于180°”
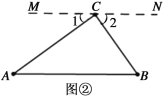
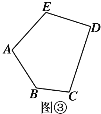
（3）拓展探究：如图③，是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
-
科目： 来源： 题型：
查看答案和解析>>【题目】概念学习
规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．
理解概念
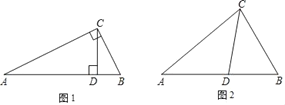
（1）如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB，请写出图中两对“等角三角形”．
概念应用
（2）如图2，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°．求证：CD为△ABC的等角分割线．
（3）在△ABC中，∠A＝42°，CD是△ABC的等角分割线，直接写出∠ACB的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，函数
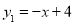的图象与函数
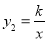（x＞0）的图象交于A（m，1），B（1，n）两点．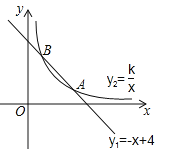
（1）求k，m，n的值；
（2）利用图象写出当x≥1时，
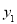和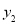
的大小关系． -
科目： 来源： 题型：
查看答案和解析>>【题目】美丽的黄河宛如一条玉带穿城而过，沿河两岸的滨河路风情线是兰州最美的景观之一．数学课外实践活动中，小林在南滨河路上的A，B两点处，利用测角仪分别对北岸的一观景亭D进行了测量．如图，测得∠DAC＝45°，∠DBC＝65°.若AB＝132米，求观景亭D到南滨河路AC的距离(结果精确到1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点．
（1）如果图中线段都可画成有向线段，那么在这些有向线段所表示的向量中，与向量
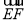相等的向量是 ；（2）设
＝
，
＝
，
＝
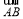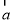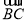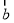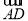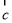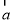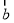．试用向量，或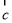表示下列向量：
＝ ；
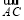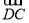＝ ．（3）求作：
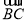
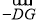．（请在原图上作图，不要求写作法，但要写出结论）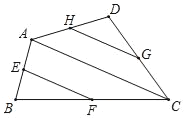
相关试题
