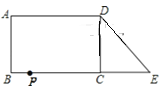
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.
参考答案:
【答案】3或13
【解析】
由条件可知BP=t,当点P在线段BC上时可知BP=CE,当点P在线段DA上时,则有AD=CE,分别可得到关于t的方程,可求得t的值.
解:因为AB=CD,若∠ABP=∠DCE=90°,BP=CE=3,根据SAS证得△ABP≌△DCE,
由题意得:BP=t=3,
所以t=3,
因为AB=CD,若∠BAP=∠DCE=90°,AP=CE=3,根据SAS证得△BAP≌△DCE,
由题意得:AP=16-t=3,
解得t=13.
所以,当t的值为3或13秒时.△ABP和△DCE全等.
故答案为: 3或13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(a,b),B(c,0),|a-3|+(2b-c)2+
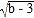 =0.
=0.
(1)求点A,B的坐标;
(2)如图,点C为x轴正半轴上一点,且OC=OA,点D为OC的中点,连AC,AD,请探索AD+CD与
 AC之间的大小关系,并说明理由;
AC之间的大小关系,并说明理由;
(3)如图,过点A作AE⊥y轴于E,F为x轴负半轴上一动点( 不与(-3,0)重合 ),G在EF延长线上,以EG为一边作∠GEN=45°,过A作AM⊥x轴,交EN于点M,连FM,当点F在x轴负半轴上移动时,式子
 的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.
的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
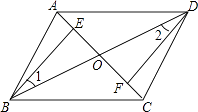
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程组:
(1)
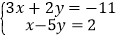 ;
; (2)
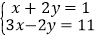 ;
;(3)
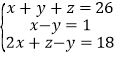 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是a m,下底都是b m,高都是(b-a) m.
(1)求小红家这块L形菜地的面积.(用含a、b的代数式表示)
(2)若a2+b2=15,ab=5,求小红家这块L形菜地的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】新新儿童服装店对“天使”牌服装进行调价,其中A型服装每件的价格上调了10%,B型服装每件的价格下调了5%,已知调价前买这两种服装各一件共花费140元,调价后买3件A型服装和2件B型服装共花费350元,则这两种服装在调价前每件各多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点D的对应点D′.
(1)根据特征画出平移后的△A′B′C′;
(2)利用网格的特征,画出AC边上的高BE并标出画法过程中的特征点;
(3)△A′B′C′的面积为 .

相关试题

