【题目】如图,在平面直角坐标系中,A(a,b),B(c,0),|a-3|+(2b-c)2+![]() =0.
=0.

(1)求点A,B的坐标;
(2)如图,点C为x轴正半轴上一点,且OC=OA,点D为OC的中点,连AC,AD,请探索AD+CD与![]() AC之间的大小关系,并说明理由;
AC之间的大小关系,并说明理由;

(3)如图,过点A作AE⊥y轴于E,F为x轴负半轴上一动点( 不与(-3,0)重合 ),G在EF延长线上,以EG为一边作∠GEN=45°,过A作AM⊥x轴,交EN于点M,连FM,当点F在x轴负半轴上移动时,式子![]() 的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.
的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.

参考答案:
【答案】(1)A(3,3),B(6,0);(2)AD+CD>![]() AC;(3)不变化,1.
AC;(3)不变化,1.
【解析】
(1)利用非负性建立方程即可得出结论;
(2)延长AD到E,使DE=AD,连接OE,先证明△ACD≌△EOD, 得到AC=OE, 再依据三角形的三边关系即可得出结论;
(3)在AM上截取AN=OF,连EH,易证△AEH≌△OEF,再根据角与角之间的关系,证明△MEH≌△MEF,则有FM=HM,即可求得该式子的值.
解:(1)∵|a-3|+(2b-c)2+![]() =0,
=0,
∴ ,解得
,解得 ,
,
∴A(3,3),B(6,0).
(2)延长AD到E,使DE=AD,连接OE,则AE=2AD,
∵AD为△ABC的中线
∴OD=CD
在△ACD和△EOD中
 ,
,
∴△ACD≌△EOD
∴AC=OE
在△AOE中,根据三角形的三边关系有
AO+OE>>AE
而OC=OA,AE=2AD
∴2CD+2AD>AC
即AD+CD>![]() AC;
AC;
(3)不变,
在AM上截取AH=OF,连接EH,
∵A(3,3),
∴OE=AE,
∵∠A=∠EOF=90°,AH=OF,
∴△AEH≌△OEF(SAS),
∴EH=EF,∠AEH=∠FEO,
∵∠AEO=90°,
∴∠HEM=90°-∠AEH-∠MEO=90°-45°=45°,
∴∠NEH=∠MEF=45°,
∵EM=EM,
∴△MEH≌△MEF(SAS),
∴FM=HM,
∴![]() =
= ![]() =
= ![]() = 1.
= 1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠DAC及∠BOA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二维码已经给我们的生活带来了很大方便,它是由大小相同的黑白两色的小正方形(如图中C型黑白一样)按某种规律组成的一个大正方形。现有25×25格式的正方形如图,角上是三个7×7的A型大黑白相间正方形,中间右下有一个5×5的B型黑白相间正方形((A,B型均由C型黑白两色小正方形组成),除这4个正方形外,其他的C型小正方形黑色块数正好是白色块数的3倍多53块,则该25×25格式的二维码中除去A、B型后,有__块C型白色小正方形,整个二维码中共有__块C型白色小正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
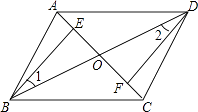
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程组:
(1)
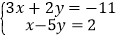 ;
; (2)
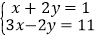 ;
;(3)
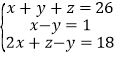 .
. -
科目: 来源: 题型:
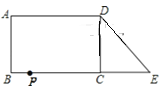
查看答案和解析>>【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.
相关试题

