【题目】如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.

(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
参考答案:
【答案】(1)4![]() m;(2)12m.
m;(2)12m.
【解析】
试题分析:(1)根据题意得出∠ADB=30°,进而利用锐角三角函数关系得出AD的长;(2)利用(1)中所求,结合CD=ADtan60°求出答案.
试题解析:(1)∵教学楼B点处观测到旗杆底端D的俯角是30°, ∴∠ADB=30°,
在Rt△ABD中,∠BAD=90°,∠ADB=30°,AB=4m, ∴AD=![]() =
=![]() =4
=4![]() (m),
(m),
答:教学楼与旗杆的水平距离是4![]() m;
m;
(2)∵在Rt△ACD中,∠ADC=90°,∠CAD=60°,AD=4![]() m,
m,
∴CD=ADtan60°=4![]() ×
×![]() =12(m),
=12(m),
答:旗杆CD的高度是12m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几种说法:①北纬30°,东经115°;②海口的南面;③第1排第4列.其中能确定位置的有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下表可知,方程x2+3x﹣5=0的一个近似解x为( )
x
1
1.1
1.2
1.3
1.4
x2+3x﹣5
﹣1
﹣0.49
0.04
0.59
1.16
A. 1.1 B. 1.2 C. 1.3 D. 1.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AB∥CD ∠1=∠2,∠3=∠4,试说明AD∥BE
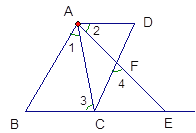
解:∵AB∥CD
∴∠4=∠BAE( )
∵∠3=∠4
∴∠3=∠BAE( )
∵∠1=∠2
∴∠ 1+∠CAF=∠2+∠CAF
即 ∠BAE=∠_____
∴∠3=∠_____
∴AD∥BE ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
⑴画出△ABC向右平移4个单位后得到的△A1B1C1;
⑵图中AC与A1C1的关系是: ;
⑶画出△ABC中AB边上的中线CD;
⑷△ACD的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,不能成为直角三角形的三条边长的是( )
A. 3,4,5B. 7,24,25C. 6,8,10D. 9,11,13
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x-5)2=x2+kx+25,则k=( )
A.5
B.-5
C.10
D.-10
相关试题

