【题目】如图, 已知反比例函数y=![]() 的图象与一次函数y=ax+b的图象交于M(2,m)和N(-1,-4)两点.
的图象与一次函数y=ax+b的图象交于M(2,m)和N(-1,-4)两点.
(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)请判断点P(4,1)是否在这个反比例函数的图象上,并说明理由.

参考答案:
【答案】(1)y=2x-2;(2)3;(3)P点在反比例函数图象上.
【解析】【试题分析】(1)将N(-1,-4)代入反比例函数解析式,即可求出反比例函数解析式;当x=2时,代入反比例函数解析式,求出点M的坐标,将M、N两点代入一次函数,构造方程组,求出k、b即可.
(2)利用分割法求面积:S△MON=S△MOA+S△NOA.
(3) 点P(4,1)的坐标代入y=![]() ,验证即可.
,验证即可.
【试题解析】
(1)由已知,得-4=![]() ,k=4,∴y=
,k=4,∴y=![]() .又∵图象过M(2,m)点,∴m=
.又∵图象过M(2,m)点,∴m=![]() =2,∵y=ax+b图象经过M、N两点,∴
=2,∵y=ax+b图象经过M、N两点,∴![]() 解之得
解之得![]() ∴y=2x-2.
∴y=2x-2.
(2)如图,对于y=2x-2,y=0时,x=1,∴A(1,0),OA=1,∴S△MON=S△MOA+S△NOA=![]() OA·MC+
OA·MC+![]() OA·ND=
OA·ND=![]() ×1×2+
×1×2+![]() ×1×4=3.
×1×4=3.
(3)将点P(4,1)的坐标代入y=![]() ,知两边相等,∴P点在反比例函数图象上.
,知两边相等,∴P点在反比例函数图象上.
-
科目: 来源: 题型:
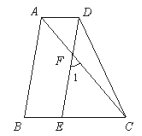
查看答案和解析>>【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中,装有10个红球、2个黄球、8个篮球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取出若干个红球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率是 ,问取出了多少个红球?
,问取出了多少个红球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的顶点A是双曲线y=
 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO= .
.(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A.C的坐标和△AOC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x+b与双曲线y=
 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>
 的解集.
的解集.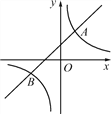
-
科目: 来源: 题型:
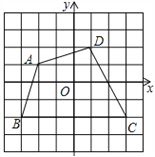
查看答案和解析>>【题目】 如图,已知四边形ABCD(网格中每个小正方形的边长均为1).
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥DE,∠1=∠ACB,AC平分∠BAD,
(1)试说明: AD∥BC.
(2)若∠B=80°,求∠ADE的度数.
相关试题

