搜索
【题目】如图，在Rt△ABC中，∠ACB=90°，点D，E分别是边AB，AC的中点，延长BC到点F，使CF= 
BC．若AB=10，则EF的长是 ． 
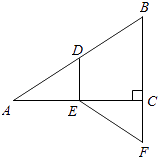
参考答案：
【答案】5
【解析】解：如图，连接DC． DE是△ABC的中位线，
∴DE∥BC，DE= 
，
∵CF= 
BC，
∴DE∥CF，DE=CF，
∴CDEF是平行四边形，
∴EF=DC．
∵DC是Rt△ABC斜边上的中线，
∴DC= 
=5，
∴EF=DC=5，
所以答案是：5．
【考点精析】关于本题考查的直角三角形斜边上的中线和三角形中位线定理，需要了解直角三角形斜边上的中线等于斜边的一半；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，E为DC边上一点，且DE=1，AE=EF，∠AEF=90°，则FC= （ ）
A.
B. 
C. 
D. 1 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在梯形ABCD中，AD∥BC，∠B=70°，∠C=40°，过点D作DE∥AB交BC于点E，若AD=3，BC=10，则CD的长是________。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AB=5，AD=3，点P是AB边上一点（不与A，B重合），连接CP，过点P作PQ⊥CP交AD于点Q，连接CQ。取CQ的中点M，连接MD，MP，若MD⊥MP，则AQ的长________。
-
科目： 来源： 题型：
查看答案和解析>>【题目】
（1）计算：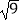
+（ 
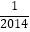）0+|﹣1|；
（2）先化简，再求值：（x+2）2+x（2﹣x），其中x=
． -
科目： 来源： 题型：
查看答案和解析>>【题目】
（1）如图1，点E，F在BC上，BE=CF，AB=DC，∠B=∠C，求证：∠A=∠D．
（2）如图2，在边长为1个单位长度的小正方形所组成的网格中，△ABC的顶点均在格点上． ①求sinB的值；
②画出△ABC关于直线l对称的△A1B1C1（A与A1 ， B与B1 ， C与C1相对应），连接AA1 ， BB1 ， 并计算梯形AA1B1B的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】设中学生体质健康综合评定成绩为x分，满分为100分，规定：85≤x≤100为A级，75≤x≤85为B级，60≤x≤75为C级，x＜60为D级．现随机抽取福海中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图，请根据图中的信息，解答下列问题：
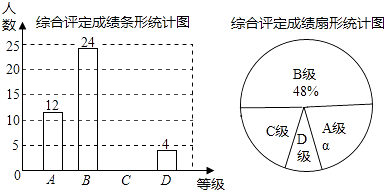
（1）在这次调查中，一共抽取了名学生，α=%；
（2）补全条形统计图；
（3）扇形统计图中C级对应的圆心角为度；
（4）若该校共有2000名学生，请你估计该校D级学生有多少名？
相关试题
