【题目】已知A、B、C三点在数轴上的位置如图所示,它们表示的数分别是a、b、c

(1) 填空:abc________0,a+b________ac,ab-ac________0;(填“>”,“=”或“<”)
(2) 若|a|=2,且点B到点A、C的距离相等
① 当b2=16时,求c的值
② 求b、c之间的数量关系
③ P是数轴上B,C两点之间的一个动点设点P表示的数为x.当P点在运动过程中,bx+cx+|x-c|-10|x+a|的值保持不变,求b的值
参考答案:
【答案】(1) < , > , > ;(2)①c=10;②c=2b+2;③b=3
【解析】
(1)根据点在数轴上的位置得到a<0<b<c,于是得到结论;
(2)①根据已知条件达到a=-2,b=4,根据点B到点A,C的距离相等,列方程即可得到结论;
②根据![]() 即可判断b、c之间的数量关系;
即可判断b、c之间的数量关系;
③依题意得原式=(b+c-11)x+10a+c当P点在运动过程中,原式的值保持不变,即原式的值与x无关,列方程组即可得到结论.
解:(1)由题中的数轴可知,a<0<b<c,且![]()
∴abc<0,a+b>0,ab-ac>0,
故答案为:<,>,>;
(2) ①![]() 且
且![]() ,
,![]() ,
,
![]() 且
且![]() ,
,![]() .
.
∵点B到点A,C的距离相等,∴![]()
∴![]() ,∴
,∴![]()
②∵![]() , ∴
, ∴![]() ,
,
③依题意,得![]()
![]()
∴原式=![]()
![]()
![]()
∵![]()
∴原式=![]() 【此处
【此处![]() 不取-2没关系】
不取-2没关系】
![]()
∵当 P 点在运动过程中,原式值保持不变,即原式的值与![]() 无关
无关
∴![]() ,∴
,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接2018年高中招生考试,某中学对全校九年级进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成如下两幅不完整的统计图1和图2,请你根据图中所给的信息解答下列问题。
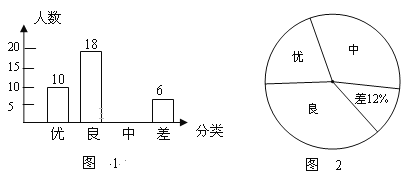
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中表示成绩为“优”的扇形所对的圆心角为 度;
(3)学校九年级共有600人参加这次数学考试,估计该校有多少名学生成绩可以达到优.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知AD∥BC,∠B=∠D=120°.
(1)请问:AB与CD平行吗?为什么?
(2)若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.
(3)若点E在直线CD上,且满足∠EAC=
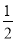 ∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).

-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年5月26日第5届中国国际大数据产业博览会召开.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )

A. 签约金额逐年增加
B. 与上年相比,2019年的签约金额的增长量最多
C. 签约金额的年增长速度最快的是2016年
D. 2018年的签约金额比2017年降低了22.98%
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正比例函数y=kx(k≠0)的图象经过点P(2,3),则该函数的图象经过的点是( )
A.(3,2)B.(1,6)C.(2,3)D.(1,6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年12月7日,第十一届全国三维数字化创新设计大赛(简称“全国3D大赛”)总决赛在玉溪启动.某学校为了解学生对这次大赛的了解程度,在全校1300名学生中随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅统计图.下列四个选项中,错误的是( )
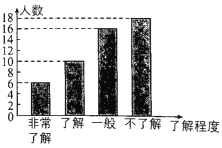
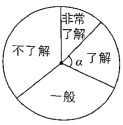
A.抽取的学生人数为50B.“非常了解”的人数占抽取的学生人数的12%
C.
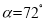 D.全校“不了解”的人数估计有428人
D.全校“不了解”的人数估计有428人 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是用图象反映的某地男女生身高生长速度y(厘米/年)与年龄x(岁)的对应关系.根据图象,有以下四个推断:

①13岁时,男生、女生的身高增长速度相同
②13岁以后,男生的身高增长速度比女生的身高增长速度快
③15岁时,男生、女生的身高增长速度达到最高值
④13岁以前,男生的身高增长速度比女生的身高增长速度快
其中合理的是( )
A.①②B.①③C.②④D.③④
相关试题

