【题目】如图,在数轴上,点![]() 表示
表示![]() ,点
,点![]() 表示
表示![]() ,点
,点![]() 表示
表示![]() .动点
.动点![]() 从点
从点![]() 出发,沿数轴正方向以每秒
出发,沿数轴正方向以每秒![]() 个单位的速度匀速运动;同时,动点
个单位的速度匀速运动;同时,动点![]() 从点
从点![]() 出发,沿数轴负方向以每秒
出发,沿数轴负方向以每秒![]() 个单位的速度匀速运动.设运动时间为
个单位的速度匀速运动.设运动时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点相遇?相遇点
两点相遇?相遇点![]() 所对应的数是多少?
所对应的数是多少?
(2)在点![]() 出发后到达点
出发后到达点![]() 之前,求
之前,求![]() 为何值时,点
为何值时,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等;
的距离相等;
(3)在点![]() 向右运动的过程中,
向右运动的过程中,![]() 是
是![]() 的中点,在点
的中点,在点![]() 到达点
到达点![]() 之前,求
之前,求![]() 的值.
的值.

参考答案:
【答案】(1)![]() ;
;![]() ;(2)3或
;(2)3或![]() ;(3)28.
;(3)28.
【解析】
(1)根据题意,由相遇时P、Q两点的路程和为28列出方程求解即可;
(2)由题意得,t的值大于0且小于7.分点P在点O的左边,点P在点O的右边两种情况讨论即可求解;
(3)根据中点的定义得到AN=PN=![]() AP=t,可得CN=AC-AN=28-t,PC=28-AP=28-2t,再代入计算即可求解.
AP=t,可得CN=AC-AN=28-t,PC=28-AP=28-2t,再代入计算即可求解.
解:(1)根据题意得2t+t=28,
解得t=![]() ,
,
∴AM=![]() >10,
>10,
∴M在O的右侧,且OM=![]() -10=
-10=![]() ,
,
∴当t=![]() 时,P、Q两点相遇,相遇点M所对应的数是
时,P、Q两点相遇,相遇点M所对应的数是![]() ;
;
(2)由题意得,t的值大于0且小于7.
若点P在点O的左边,则10-2t=7-t,解得t=3.
若点P在点O的右边,则2t-10=7-t,解得t=![]() .
.
综上所述,t的值为3或![]() 时,点P到点O的距离与点Q到点B的距离相等;
时,点P到点O的距离与点Q到点B的距离相等;
(3)∵N是AP的中点,
∴AN=PN=![]() AP=t,
AP=t,
∴CN=AC-AN=28-t,PC=28-AP=28-2t,
2CN-PC=2(28-t)-(28-2t)=28.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式2x+4y+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,DEF分别为△ABC边ACABBC上的点,∠A=∠1=∠C,DE=DF.下面的结论一定成立的是( )
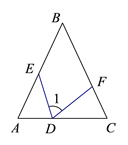
A. AE=FC B. AE=DE C. AE+FC=AC D. AD+FC=AB
-
科目: 来源: 题型:
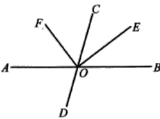
查看答案和解析>>【题目】如图,直线
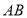 与
与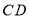 相交于点
相交于点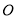 ,
,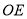 是
是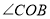 的平分线,
的平分线,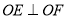 ,.
,.(1)图中∠BOE的补角是
(2)若∠COF=2∠COE,求
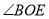 的度数;
的度数;(3) 试判断OF是否平分∠AOC,并说明理由;请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市自实施《生活垃圾分类和减量管理办法》以来,生活垃圾分类和减量工作取得了一定的成效,环保部门为了提高 宣传实效,随机抽样调查了100户居民8月的生活垃圾量,并绘制成不完整的扇形统计图,请你根据图中的信息解答下列问题
(1)请将条形统计图22-(1)补充完整.
(2)在图22-(2)的扇形统计图中,求表示“有害垃圾C”所在扇形的圆心角的度数.
(3)根据统计,8月所抽查的居民产生的生活垃圾总量为2750kg,则其中为可回收垃圾约为多少kg?



-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意有理数a,b,
定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算.例如,2⊙5=2(2+5)﹣1=13.
(Ⅰ)求[1⊙(﹣2)]⊙3
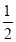 的值;
的值;(Ⅱ)对于任意有理教m,n请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n=_____.(用含m,n的式子表示)
相关试题

