【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式2x+4y+1的值.
参考答案:
【答案】(1)2;(2)![]() ;(3)9.
;(3)9.
【解析】
(1)直接利用新定义即可即可得出结论;
(2)先利用新定义得出(-3)⊕x=3x-6,(x+1)⊕5=-3x-3,进而建立方程求解即可得出结论;
(3)先利用新定义得出x⊕1=x,2(1⊕y)=-2y+4进而建立方程得出x+2y=4,即可得出结论.
解:(1)∵a⊕b=2a-ab,
∴(-2)⊕3=2×(-2)-(-2)×3=2.
(2)由题意知,(-3)⊕x=2×(-3)-(-3)x=3x-6,
(x+1)⊕5=2(x+1)-5(x+1)=-3x-3,
∵(-3)⊕x=(x+1)⊕5,
∴3x-6=-3x-3,
∴x=![]() .
.
(3)由题意知,x⊕1=2x-x=x,2(1⊕y)=2(2×1-y)=-2y+4,
∵x⊕1=2(1⊕y),
∴x=-2y+4,
∴x+2y=4,
∴2x+4y+1=2(x+2y)+1=9.
-
科目: 来源: 题型:
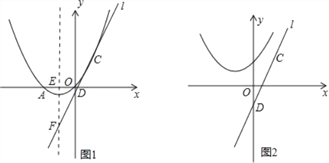
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过原点O及点A(﹣4,0)和点C(2,3).
(1)求抛物线的解析式及顶点坐标;
(2)如图1,设抛物线的对称轴与x轴交于点E,将直线y=2x沿y轴向下平移n个单位后得到直线l,若直线l经过C点,与y轴交于点D,且与抛物线的对称轴交于点F.若P是抛物线上一点,且PC=PF,求点P的坐标;
(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,求新抛物线上到直线CD距离最短的点的坐标.(直接写出结果,不要解答过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标平面内,
 为原点,点
为原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为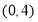 ,直线
,直线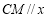 轴. 点
轴. 点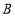 与点
与点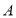 关于原点对称,直线
关于原点对称,直线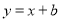 (
(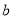 为常数)经过点
为常数)经过点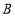 ,且与直线
,且与直线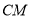 相交于点
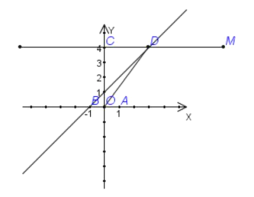
相交于点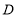 .
.
(1)求
 的值和点
的值和点 的坐标;
的坐标;(2)在
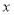 轴上有一点
轴上有一点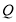 ,使
,使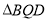 的面积为
的面积为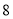 ,求
,求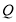 点的坐标;
点的坐标; (3)在
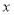 轴的正半轴上是否存在一点
轴的正半轴上是否存在一点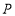 ,使得
,使得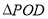 为等腰三角形,若存在,求出点
为等腰三角形,若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】直接写出结果:
(1)6+(﹣9)=_____.
(2)﹣5﹣15=____.
(3)12÷(﹣3)=____.
(4)
 =______.
=______.(5)
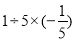 =______.
=______.(6)(﹣2)2018+(﹣2)2017=______.
(7)﹣3a2+2a2=_____.
(8)﹣2(x﹣1)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,DEF分别为△ABC边ACABBC上的点,∠A=∠1=∠C,DE=DF.下面的结论一定成立的是( )
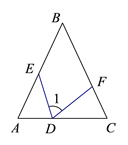
A. AE=FC B. AE=DE C. AE+FC=AC D. AD+FC=AB
-
科目: 来源: 题型:
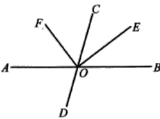
查看答案和解析>>【题目】如图,直线
 与
与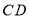 相交于点
相交于点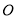 ,
,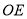 是
是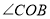 的平分线,
的平分线,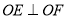 ,.
,.(1)图中∠BOE的补角是
(2)若∠COF=2∠COE,求
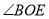 的度数;
的度数;(3) 试判断OF是否平分∠AOC,并说明理由;请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点
 表示
表示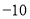 ,点
,点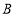 表示
表示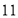 ,点
,点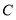 表示
表示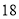 .动点
.动点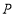 从点
从点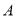 出发,沿数轴正方向以每秒
出发,沿数轴正方向以每秒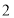 个单位的速度匀速运动;同时,动点
个单位的速度匀速运动;同时,动点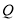 从点
从点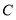 出发,沿数轴负方向以每秒
出发,沿数轴负方向以每秒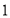 个单位的速度匀速运动.设运动时间为
个单位的速度匀速运动.设运动时间为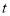 秒.
秒.(1)当
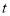 为何值时,
为何值时,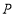 、
、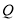 两点相遇?相遇点
两点相遇?相遇点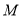 所对应的数是多少?
所对应的数是多少?(2)在点
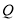 出发后到达点
出发后到达点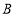 之前,求
之前,求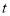 为何值时,点
为何值时,点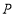 到点
到点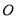 的距离与点
的距离与点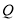 到点
到点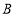 的距离相等;
的距离相等;(3)在点
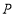 向右运动的过程中,
向右运动的过程中,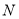 是
是 的中点,在点
的中点,在点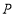 到达点
到达点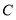 之前,求
之前,求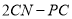 的值.
的值.
相关试题

