【题目】如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AC平分∠BAD,求证:ABCD为菱形.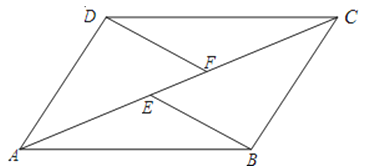
参考答案:
【答案】证明:(1)∵DF∥BE,
∴∠DFA=∠CEB,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在△ADF和△CBE中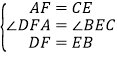 ,
,
∴△ADF≌△CBE(SAS),
∴AD=CB,∠DAC=∠ACB,
∴AD∥CB,
∴四边形ABCD是平行四边形;
(2)∵AC平分∠BAD,
∴∠DAC=∠BAC,
∴∠BAC=∠ACB,
∴AB=BC,
∴ABCD为菱形.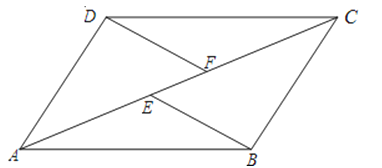
【解析】(1)首先证明△ADF≌△CBE,根据全等三角形的性质可得AD=CB,∠DAC=∠ACB,进而可得证明AD∥CB,根据一组对边平行且等的四边形是平行四边形可得四边形ABCD是平行四边形;
(2)首先根据角平分线的性质可得∠DAC=∠BAC,进而可得出AB=BC,再根据一组邻边相等的平行四边形是菱形可得结论.
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,属于必然事件的是( )
A.三角形的内心到三角形三个顶点的距离相等B.重心有可能在三角形外
C.外心是三角形三条角平分线的交点D.等边三角形的内心与外心重合
-
科目: 来源: 题型:
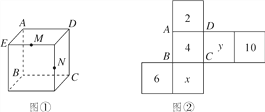
查看答案和解析>>【题目】如图所示,图①为一个正方体,其棱长为10,图②为图①的表面展开图(数字和字母写在外表面上,字母也可以表示数),请根据要求回答问题:
(1)如果正方体相对面上的两个数字之和相等,则x=________,y=________;
(2)如果面“2”是右面,面“4”在后面,则上面是________(填“6”“10”“x”或“y”);
(3)图①中,M,N为所在棱的中点,试在图②中找出点M,N的位置,并求出图②中三角形ABM的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】太阳中心的温度可达15500000℃,这个数用科学记数法表示正确的是( )
A. 0.155×108B. 15.5×106C. 1.55×107D. 1.55×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3xy3的系数是 , 次数是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,直线L垂直分线段AC,垂足为O,直线L分别于线段AD,CB的延长线交于点E,F,证明四边形AFCE是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列式子:1⊕3=1×2+3=5,3⊕1=3×2+1=7,5⊕4=5×2+4=14.请你想一想:(a﹣b)⊕(a+b)=_____.(用含a,b的代数式表示)
相关试题

