【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,边AB、OA(AB>OA)的长分别是方程x2﹣11x+24=0的两个根,D是AB上的点,且满足![]() .
.
(1)矩形OABC的面积是 ,周长是 .
(2)求直线OD的解析式;
(3)点P是射线OD上的一个动点,当△PAD是等腰三角形时,求点P的坐标.

参考答案:
【答案】(1)S=24,C=22;(2)y=-x;(3)P点的坐标为(![]() ,
, ![]() );(0,0);
);(0,0);  ;
; 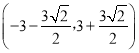
【解析】试题分析:(1)根据边AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,即可得到AO=3,AB=8,进而得出矩形OABC的面积以及矩形OABC的周长;
(2)根据![]() ,AB=8,可得AD=3,再根据AO=3,进而得出D(-3,3),再根据待定系数法即可求得直线OD的解析式;
,AB=8,可得AD=3,再根据AO=3,进而得出D(-3,3),再根据待定系数法即可求得直线OD的解析式;
(3)根据△PAD是等腰三角形,分情况讨论,根据等腰直角三角形的性质,求得点P的坐标.
试题解析:(1)(1)∵x2-11x+24=0,
∴(x-3)(x-8)=0,
∴x1=3,x2=8,
∵AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,
∴AO=3,AB=8,
∴矩形OABC的面积=3×8=24,矩形OABC的周长=2×(3+8)=22,
故答案为:24,22;
(2)∵![]() ,AB=8,
,AB=8,
∴AD=3,
又∵AO=3,
∴D(-3,3),
设直线OD解析式为y=kx,则
3=-3k,即k=-1,
∴直线OD的解析式为y=-x;
(3)∵AD=AO=3,∠DAO=90°,
∴△AOD是等腰直角三角形,
∴∠ADO=45°,DO=3![]() ,
,
根据△PAD是等腰三角形,分4种情况讨论:
①如图所示,当AD=AP1=3时,点P1的坐标为(0,0);
②如图所示,当DA=DP2=3时,过P2作x轴的垂线,垂足为E,则
OP2=3![]() -3,△OEP2是等腰直角三角形,
-3,△OEP2是等腰直角三角形,
∴P2E=OE=![]() =3-
=3-![]() ,
,
∴点P2的坐标为(-3+![]() ,3-
,3-![]() );
);
③如图所示,当AP3=DP3时,∠DAP3=∠ADO=45°,
∴△ADP3是等腰直角三角形,
∴DP3=![]() =
=![]()
∴P3O=3![]() -
-![]() =
=![]() ,
,
过P3作x轴的垂线,垂足为F,则△OP3F是等腰直角三角形,
∴P3F=OF=![]() ,
,
∴点P3的坐标为(-![]() ,
, ![]() );
);
④如图所示,当DA=DP4=3时,P4O=3+3![]() ,
,
过P4作x轴的垂线,垂足为G,则△OP4G是等腰直角三角形,
∴P4G=OG=![]() +3,
+3,
∴点P4的坐标为(-3-![]() ,3+
,3+![]() );
);
综上所述,P点的坐标为(![]() ,
, ![]() );(0,0);
);(0,0); ![]() ;
; ![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=
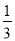 ∠ABC,∠OCB=
∠ABC,∠OCB=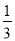 ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.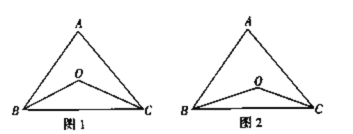
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月,某校为了了解九年级学生的体育备考情况,随机抽取了部分学生进行模拟测试,现将学生按模拟测试成绩m分成A、B、C、D四等(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60),并绘制出了如图的两幅不完整的统计图:

(1)本次模拟测试共抽取了多少个学生?
(2)将图乙中条形统计图补充完整;
(3)如果该校今年有九年级学生1000人,试估计其中D等学生的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°.
(1)求证:EF=BE+DF;
(2)若线段EF、AB的长分别是方程x2﹣5x+6=0的两个根,求△AEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:

经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级举行数学竞赛,学校准备购买甲、乙、丙三种笔记本奖励给获奖学生,已知甲种笔记本单价比乙种笔记本单价高10元,丙种笔记本单价是甲种笔记本单价的一半,单价和为80元.
(1)甲、乙、丙三种笔记本的单价分别是多少元?
(2)学校计划拿出不超过950元的资金购买三种笔记本40本,要求购买丙种笔记本20本,甲种笔记本超过5本,有哪几种购买方案?
相关试题

