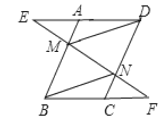
【题目】已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E、F,且AE=CF.
(1) 求证:△AEM≌△CFN.
(2) 求证:四边形BNDM是平行四边形.
参考答案:
【答案】(1)见详解;(2)见详解.
【解析】
(1)根据四边形ABCD是平行四边形,证明∠E=∠F,∠EAM=∠FNC,结合AE=CF,问题得证;
(2)根据△AEM≌△CFN和据四边形ABCD是平行四边形,证明BM=DN,BM∥DN,问题得证.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠BAD=∠BCD,
∴∠E=∠F,∠EAM=∠FNC,
∵AE=CF,
∴△AEM≌△CFN;
(2)证明:∵△AEM≌△CFN,
∴AM=CN,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴BM=DN,
∴四边形BNDM是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应市委政府“加快建设美丽江城”的号召,我市某街道决定从备选的五种树中选购--种进行栽种。为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

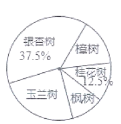
请根据所给信息解答以下问题:
(1)这次参与调查的居民总人数是多少人?
(2)此次调查的居民中最喜欢樟树的有多少人?请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为等边三角形,
为等边三角形, ,
, 、
、 相交于点
相交于点 ,
, 于点
于点 ,
, ,
, .
.(1)求证:
 ;
;(2)求
 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车去韶山研学, 现有甲、乙两种大客车,甲种客车每辆载客量
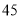 人,乙种客车每辆载客量
人,乙种客车每辆载客量 人.已知
人.已知 辆甲种客车和
辆甲种客车和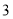 辆乙种客车需租金
辆乙种客车需租金 元,
元,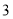 辆甲种客车和
辆甲种客车和 辆乙种客车共需租金
辆乙种客车共需租金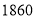 元.
元.(1)求
 辆甲种客车和
辆甲种客车和 辆乙种客车的租金分别是多少元?
辆乙种客车的租金分别是多少元?(2)学校计划租用甲、乙两种客车共
 辆,送
辆,送 名师生集体外出活动,总费用不超过
名师生集体外出活动,总费用不超过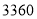 元,则共有哪几种租车方案?
元,则共有哪几种租车方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价
 (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)(2)当每盒售价定为多少元时,每天销售的利润
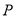 (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,以AB为直角边作等腰直角三角形ABD,与BC边交于点E,
(1)若∠ACE=18°,则∠ECD=
(2)探索:∠ACE与∠ACD有怎样的数量关系?猜想并证明.
(3)如图2,作△ABC的高AF并延长,交BD于点G,交CD延长线于点H,求证:CH2+DH2=2AD2.

相关试题

