【题目】如图,在□ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的长.

参考答案:
【答案】(1)见解析;(2)2![]() .
.
【解析】试题分析:(1)根据平行四边形的性质求出AO=OC,BO=OD,求出AC=BD,根据矩形的判定推出即可;
(2)根据矩形性质求出∠ABC=90°,求出∠CAB=30°,解直角三角形求出即可.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵OA=OB,
∴OA=OB=OC=OD,
∴AC=BD,
∴四边形ABCD是矩形;
(2)解:∵∠AOB=120°,OA=OB,
∴∠OAB=∠OBA=30°,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AC=2BC,
∴AB= ![]() ,
,
∴BC=![]() AB=6×
AB=6×![]() =2
=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为等边三角形,
为等边三角形, ,
, 、
、 相交于点
相交于点 ,
, 于点
于点 ,
, ,
, .
.(1)求证:
 ;
;(2)求
 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车去韶山研学, 现有甲、乙两种大客车,甲种客车每辆载客量
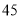 人,乙种客车每辆载客量
人,乙种客车每辆载客量 人.已知
人.已知 辆甲种客车和
辆甲种客车和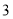 辆乙种客车需租金
辆乙种客车需租金 元,
元,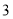 辆甲种客车和
辆甲种客车和 辆乙种客车共需租金
辆乙种客车共需租金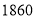 元.
元.(1)求
 辆甲种客车和
辆甲种客车和 辆乙种客车的租金分别是多少元?
辆乙种客车的租金分别是多少元?(2)学校计划租用甲、乙两种客车共
 辆,送
辆,送 名师生集体外出活动,总费用不超过
名师生集体外出活动,总费用不超过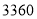 元,则共有哪几种租车方案?
元,则共有哪几种租车方案? -
科目: 来源: 题型:
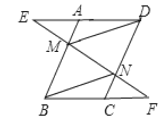
查看答案和解析>>【题目】已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E、F,且AE=CF.
(1) 求证:△AEM≌△CFN.
(2) 求证:四边形BNDM是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价
 (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)(2)当每盒售价定为多少元时,每天销售的利润
 (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,以AB为直角边作等腰直角三角形ABD,与BC边交于点E,
(1)若∠ACE=18°,则∠ECD=
(2)探索:∠ACE与∠ACD有怎样的数量关系?猜想并证明.
(3)如图2,作△ABC的高AF并延长,交BD于点G,交CD延长线于点H,求证:CH2+DH2=2AD2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:二元一次方程
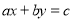 有无数组解,每组解记为
有无数组解,每组解记为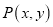 ,称
,称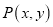 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:(1) 已知
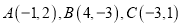 ,则是隐线
,则是隐线 的亮点的是 ;
的亮点的是 ;(2) 设
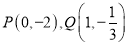 是隐线
是隐线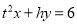 的两个亮点,求方程
的两个亮点,求方程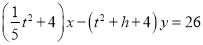 中
中 的最小的正整数解;
的最小的正整数解;(3)已知
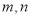 是实数, 且
是实数, 且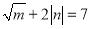 ,若
,若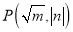 是隐线
是隐线 的一个亮点,求隐线
的一个亮点,求隐线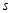 中的最大值和最小值的和.
中的最大值和最小值的和.
相关试题

