【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:∵抛物线的对称轴为直线x=﹣ ![]() =2,
=2,
∴b=﹣4a,即4a+b=0,(故①正确);
∵当x=﹣3时,y<0,
∴9a﹣3b+c<0,
即9a+c<3b,(故②错误);
∵抛物线与x轴的一个交点为(﹣1,0),
∴a﹣b+c=0,
而b=﹣4a,
∴a+4a+c=0,即c=﹣5a,
∴8a+7b+2c=8a﹣28a﹣10a=﹣30a,
∵抛物线开口向下,
∴a<0,
∴8a+7b+2c>0,(故③正确);
∵对称轴为直线x=2,
∴当﹣1<x<2时,y的值随x值的增大而增大,
当x>2时,y随x的增大而减小,(故④错误).
故选:B.
根据抛物线的对称轴为直线x=﹣ ![]() =2,则有4a+b=0;观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时,y随x的增大而减小.
=2,则有4a+b=0;观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时,y随x的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课
A
B
C
D
E
F
人数
20
30
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )

A.2
B.

C.
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】你认为月球上有水吗?如图是对某中学八年级的140名男生的调查结果.

(1)认为“有水”的频数为________,认为“没有水”的频数是_______,认为“不知道”的频数是_______;
(2)认为“有水”的频率为_______,认为“没有水”的频率是______,认为“不知道”的频率是_______,频率之和为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某中学八年级的1000名学生最喜欢的球类活动统计表:
最喜欢的
球类活动
篮球
排球
足球
乒乓球
其他
人数
185
175
260
330
50
(1)哪种球类运动最受欢迎?
(2)哪两种球类运动受欢迎的程度差不多?
(3)八年级学生最喜欢的各类球类活动的频率各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图:
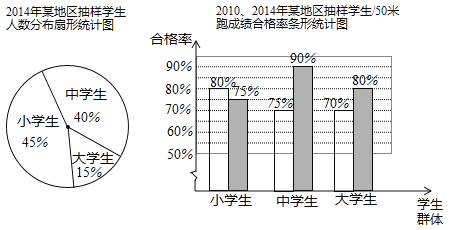
(1)本次检测抽取了大、中、小学生共 名,其中小学生 名;
(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为 名;
(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为6,E为BC上的一点,BE=2,F为AB上的一点,AF=3,P为AC上一点,则PF+PE的最小值为 .

相关试题

