【题目】如图,已知一次函数y=mx+n的图像与x轴交于点B,与反比例函数![]() (k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(1)若OA=11,求k的值;
(2)沿着x轴向右平移直线BC,若直线经过H点时恰好又经过点D,求一次函数函数y=mx+n的表达式.

参考答案:
【答案】(1)k=18;(2)![]() .
.
【解析】
(1)由∠HCB=∠HCA及CH⊥x轴得到△CHB≌△CHA,推出BH=HA=8,由BC=6根据勾股定理求出CH,由OA=11进而得出C点坐标,求得k值;
(2)过D点作DN⊥x轴于N点,由H是AB中点且HD∥BC得到D是AC的中点,设C点坐标,进而表示出D点坐标,根据k相等即可建立方程求解.
解:(1)∵CH⊥x轴
∴∠CHB=∠CHA=90°
在△CHB和△CHA中
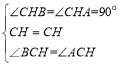 ,∴△CHB≌△CHA(ASA)
,∴△CHB≌△CHA(ASA)
∴BH=AH=![]() AB=8
AB=8
在△BCH中,由勾股定理可知:![]()
且OH=OA-AH=11-8=3
故C点的坐标为:(3,6)
∴反比例的k=3×6=18.
故答案为:18.
(2) 过D点作DN⊥x轴于N点,如下图所示:
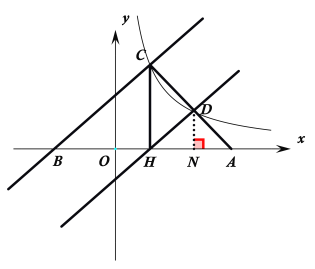
设C点坐标为(a,6),∴OH=a,CH=6
由HD∥BC,且H是AB的中点可知
HD是△ABC的中位线,且D是AC的中点
又DN⊥CH,∴DN∥CH
∴DN是△ACH的中位线
∴DN=![]() CH=4,HN=NA=
CH=4,HN=NA=![]() AH=4
AH=4
∴ON=OH+HN=a+4
∴D点的坐标为(a+4,3)
又∵C、D均在反比例函数上,
∴6×a=(a+4)×3
解之得:a=4,故C点坐标为(4,6)
BO=BH-OH=8-4=4,故B点坐标为(-4,0)
将C(4,6)和B(-4,0)代入y=mx+n中:
![]() ,解之得:
,解之得:![]()
故一次函数的解析式为:![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为预防疾病,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量
 (mg)与燃烧时间
(mg)与燃烧时间 (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后,  与
与 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:(1)求药物燃烧时
 与
与 的函数关系式.(2)求药物燃烧后
的函数关系式.(2)求药物燃烧后 与
与 的函数关系式.
的函数关系式.(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个服装厂加工同种型号的防护服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工600套防护服,甲厂比乙厂要少用4天.
(1)求甲、乙两厂每天各加工多少套防护服?
(2)已知甲、乙两厂加工这种防护服每天的费用分别是150元和120元,疫情期间,某医院紧急需要3000套这种防护服,甲厂单独加工一段时间后另有安排,剩下任务只能由乙单独完成.如果总加工费不超过6360元,那么甲厂至少要加工多少天?
-
科目: 来源: 题型:
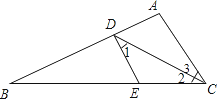
查看答案和解析>>【题目】如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数
 的图象上.
的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC的表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

相关试题

