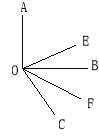
【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC.

(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
参考答案:
【答案】(1)45°;(2)∠EOF=![]() ∠AOB;(3)52°.
∠AOB;(3)52°.
【解析】
试题分析:(1)先求出∠AOC的度数,再根据角平分线的定义求出∠EOC与∠COF的度数,然后相减即可得解;
(2)设∠COF=x,∠EOB=y,先用x,y表示出∠EOF,再用x,y表示出∠AOB,然后得出两者的关系;
(3)根据(2)的规律,∠EOF的度数等于∠AOB的一半,进行求解即可.
试题解析:(1)∵∠AOB是直角,∠BOC=60°,∴∠AOC=∠AOB+∠BOC=90°+60°=150°,∵OE平分∠AOC,OF平分∠BOC,∴∠EOC=![]() ∠AOC=
∠AOC=![]() ×150°=75°,∠COF=
×150°=75°,∠COF=![]() ∠BOC=
∠BOC=![]() ×60°=30°,∴∠EOF=∠EOC﹣∠COF=75°﹣30°=45°;
×60°=30°,∴∠EOF=∠EOC﹣∠COF=75°﹣30°=45°;
(2)设∠COF=x,∠EOB=y,∵OE平分∠AOC,OF平分∠BOC,∴∠BOF= x,∠AOE=∠EOC=2x+y,∴∠EOF=x+y,∠AOB=2x+2y,∴∠EOF=![]() ∠AOB;
∠AOB;
(3)∵∠EOF=![]() ∠AOB,∴∠AOB=2∠EOF,∵∠AOB+∠EOF=156°,∴3∠EOF=156°,∴∠EOF=52°.
∠AOB,∴∠AOB=2∠EOF,∵∠AOB+∠EOF=156°,∴3∠EOF=156°,∴∠EOF=52°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
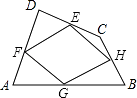
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.AB=DC -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的内角和是其外角和的一半,那么这个多边形是( )
A. 六边形 B. 五边形 C. 四边形 D. 三角形
-
科目: 来源: 题型:
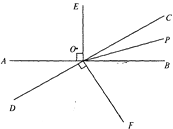
查看答案和解析>>【题目】.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,
(1)图中除直角外,还有相等的角吗?请写出两对:①____________;②____________.
(2)如果∠AOD=40°,则①∠BOC=_______;②OP是∠BOC的平分线,所以∠COP=______度;
③求∠BOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+2x+3的对称轴是( )
A.直线x=1
B.直线x=﹣1
C.直线x=﹣2
D.直线x=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的边长分别是3cm和7cm,则它的周长是____________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知两个不同的一元二次方程的判别式互为相反数,下列判断正确的是( )
A.两个方程一定都有解B.两个方程一定没有解
C.两个方程一定有公共解D.两个方程至少一个方程有解.
相关试题

