【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,且∠DAE=90°,连接CE.

(1)如图①,当点D在线段BC上时:
①BC与CE的位置关系为 ;
②BC、CD、CE之间的数量关系为 .
(2)如图②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若不成立,请你写出正确结论,并给予证明.
(3)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为 .
参考答案:
【答案】(1)①BC⊥CE;②BC=CD+CE;(2)结论①成立,②不成立,结论:CD=BC+CE;(3)CE=BC+CD.
【解析】
(1)①利用条件求出△ABD≌△ACE,随之即可得出位置关系.
②根据BD=CE,可得BC=BD+CD=CE+CD.
(2)根据第二问的条件得出△ABD≌△ACE,随之即可证明结论是否成立.
(3)分析新的位置关系得出△ABD≌△ACE,即可得出CE=BC+CD.
(1)如图1.
∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE.在△ABD和△ACE中,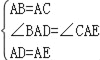 ,∴△ABD≌△ACE(SAS),∴BD=CE,∠B=∠ACE=45°,①∵∠ACE=45°=∠ACB,∴∠BCE=45°+45°=90°,即BD⊥CE;
,∴△ABD≌△ACE(SAS),∴BD=CE,∠B=∠ACE=45°,①∵∠ACE=45°=∠ACB,∴∠BCE=45°+45°=90°,即BD⊥CE;
②∵BD=CE,∴BC=BD+CD=CE+CD.
故答案为:BC⊥CE,BC=CD+CE;
(2)结论①成立,②不成立,结论:CD=BC+CE
理由:如图2中,∵∠BAC=∠DAE=90°,∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,即∠BAD=∠EAC.在△ABD和△ACE中,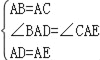 ,∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABD=135°,∴CD=BC+BD=BC+CE
,∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABD=135°,∴CD=BC+BD=BC+CE
∵∠ACB=45°
∴∠DCE=90°,∴CE⊥BC;
(3)如图3中,∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD
即∠BAD=∠CAE,∴在△ABD和△ACE中,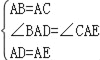 ,∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABC.
,∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABC.
∵AB=AC,∴∠ABC=∠ACB=45°,∴BD=BC+CD,即CE=BC+CD.
故答案为:CE=BC+CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.

(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解南通市80万市民“获取新闻的最主要途径”,某市记者开展了一次调查,根据调查结果绘制了如下尚不完整的统计图.
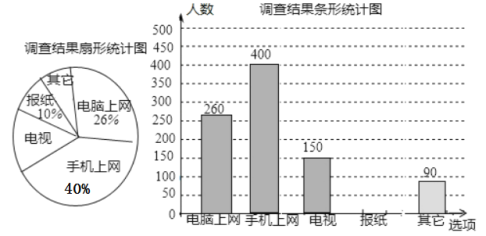
根据以上信息解答下列问题:
(1)这次调查适合采用_____________的调查方式(填“全面调查”或“抽样调查”);
(2)这次调查样本容量是____________.
(3)扇形统计图中,“电视”所对应的圆心角的度数是____________;
(4)条形统计图中“报纸”对应的人数是____________;
(5)南通市约有80万人,请估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=
 (x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .
(x>0)的图象经过AB的中点F和DE的中点G,则k的值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )

A. 10cm B. 12cm C. 15cm D. 17cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
 ,其中x的值从不等式组
,其中x的值从不等式组 的整数解中选取.
的整数解中选取. -
科目: 来源: 题型:
查看答案和解析>>【题目】以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.

(1)试判断BD、CE的数量关系,并说明理由;
(2)延长BD交CE于点F试求∠BFC的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
相关试题

